单选题 (共 8 题 ),每题只有一个选项正确
则下列结论中不正确的是
$\text{A.}$ $\sigma$ 越小,该物理量在一次测量中落在 $(9.9,10.1)$ 内的概率越大
$\text{B.}$ 该物理量在一次测量中大于 10 的概率为 0.5
$\text{C.}$ 该物理量在一次测量中小于 9.99 与大于 10.01 的概率相等
$\text{D.}$ 该物理量在一次测量中结果落在 $(9.9,10.2)$ 与落在 $(10,10.3)$ 的概率相等
已知随机变量 $\xi$ 服从正态分布 $N\left(0, \sigma^{2}\right)$ ,若 $P(\xi>2)=0.023$ ,则 $P(-2 \leq \xi \leq 2)=$
$\text{A.}$ 0.977
$\text{B.}$ 0.954
$\text{C.}$ 0.5
$\text{D.}$ 0.023
某校高三年级有 1000 人参加期末考试,经统计发现数学成绩近似服从正态分布 $N\left(120, \sigma^{2}\right)$ ,且成绩不低于 140 分的人数为 100 ,则此次考试数学成绩高于 100 分的人数约为( )
$\text{A.}$ 700
$\text{B.}$ 800
$\text{C.}$ 900
$\text{D.}$ 950
设随机变量 $\mathrm{X} \sim \mathrm{N}\left(\mu, \sigma^{2}\right)$ ,则"$\mu \geqslant 1$"是" $\mathrm{P}(\mathrm{X} < 2) < \frac{1}{2}$"的( )
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分又不必要条件
已知随机变量 $X$ 服从正态分布 $N\left(4, \sigma^{2}\right)$ ,且 $P(3 \leq X \leq 5)=0.86$ ,则 $P(X < 3)=$
$\text{A.}$ 0.43
$\text{B.}$ 0.28
$\text{C.}$ 0.14
$\text{D.}$ 0.07
已知参加 2020 年某省夏季高考的 53 万名考生的成绩 $Z$ 近似地服从正态分布 $N\left(453,99^{2}\right)$ ,估计这些考生成绩落在 $(552,651]$ 的人数约为( )
$\text{A.}$ 36014
$\text{B.}$ 72027
$\text{C.}$ 108041
$\text{D.}$ 168222
现实世界中的很多随机变量遵循正态分布。例如反复测量某一个物理量,其测量误差 $X$通常被认为服从正态分布。若某物理量做 $n$ 次测量,最后结果的误差,$X_{n} \sim N\left(0, \frac{2}{n}\right)$ ,则为使 $\left|X_{n}\right| \geqslant \frac{1}{4}$ 的概率控制在 0.0456 以下,至少要测量的次数为( )
(附)随机变量 $X \sim N\left(\mu, \sigma^{2}\right)$ ,则 $P(\mu-\sigma < X < \mu+\sigma)=0.6826, P(\mu-2 \sigma < X < \mu+2 \sigma)= 0.9544, \quad P(u-3 \sigma < X < \mu+3 \sigma)=0.9974$ .
$\text{A.}$ 32
$\text{B.}$ 64
$\text{C.}$ 128
$\text{D.}$ 256
设 $X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right)$ ,这两个正态分布密度曲线如图所示.下列结论中正确的是
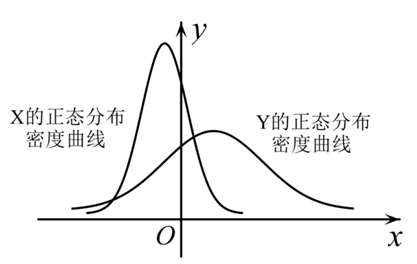
$\text{A.}$ $P\left(Y \geq \mu_2\right) \geq P\left(Y \geq \mu_1\right)$
$\text{B.}$ $P\left(X \leq \sigma_2\right) \leq P\left(X \leq \sigma_1\right)$
$\text{C.}$ 对任意正数 $t, P(X \leq t) \geq P(Y \leq t)$
$\text{D.}$ 对任意正数 $t, P(X \geq t) \geq P(Y \geq t)$
多选题 (共 3 题 ),每题有多个选项正确
已知某校高二男生的身高 $X$(单位: cm )服从正态分布 $N(175,16)$ ,且 $P(\mu-2 \sigma < X \leq \mu+2 \sigma)=0.9544$ ,则
$\text{A.}$ 该校高二男生的平均身高是 175 cm
$\text{B.}$ 该校高二男生身高的方差为 4
$\text{C.}$ 该校高二男生中身高超过 183 cm 的人数超过总数的 $3 \%$
$\text{D.}$ 从该校高二男生中任选一人,身高超过 180 cm 的概率与身高不超过 170 cm 的概率相等
给出下列命题,其中正确的是
$\text{A.}$ 对于独立性检验 $K^{2}$ 的值越大,说明两事件相关程度越大.
$\text{B.}$ 若随机变量 $\xi \sim N\left(1, \sigma^{2}\right), P(\xi \leq 4)=0.75$ ,则 $P(\xi \leq-2)=0.25$
$\text{C.}$ 若 $X \sim B\left(9, \frac{1}{3}\right)$ ,则 $D(2 X+1)=8$
$\text{D.}$ 已知样本点 $\left(x_{i}, y_{i}\right)(i=1,2,3 \mathrm{~K} 10)$ 组成一个样本,得到回归直线方程 $\hat{y}=2 x-0.4$ ,且 $\bar{x}=2$ ,剔除两个样本点 $(-3,1)$ 和 $(3,-1)$ 得到新的回归直线的斜率为 3 ,则新的回归方程为
$\hat{y}=3 x-3$
下列命题中正确的是( )
$\text{A.}$ 已知一组数据 $6, ~ 6, ~ 7, ~ 8, ~ 10, ~ 12$ ,则这组数据的 $50 \%$ 分位数是 7.5
$\text{B.}$ 已知随机变量 $X \sim N\left(2, \sigma^{2}\right)$ ,且 $P(X>3)=0.3$ ,则 $P(1 < X < 2)=0.2$
$\text{C.}$ 已知随机变量 $Y \sim B\left(10, \frac{1}{2}\right)$ ,则 $E(Y)=\frac{5}{2}$
$\text{D.}$ 已知经验回归方程 $\$=-2 x+3$ ,则 $y$ 与 $x$ 具有负线性相关关系
填空题 (共 2 题 ),请把答案直接填写在答题纸上
已知随机变量 $X$ 服从正态分布 $\mathrm{N}\left(1, \sigma^{2}\right)$ ,若 $P(X>a)=P(X < a)$ ,则 $a=$
设随机变量 $X \sim N\left(72, \sigma^{2}\right)$ ,若 $P(70 < X < 73)=0.3$ ,则 $P(71 < X < 74)=$
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
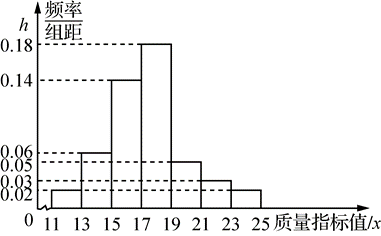
从某企业的某种产品中抽取 500 件,测量这些产品的一项质量指标值,由测量结果得如下频率直方图:
(1)求这 500 件产品质量指标值的样本平均数 $\overline{ x }$ 和样本方差 $s ^2$(同一组数据用该区间的中点值作代表,记作 $x _{ i }, i =1,2, \cdots, 7$ );
(2)由频率直方图可以认为,这种产品的质量指标值 X 服从正态分布 $N \left(\mu, \sigma^2\right)$ ,其中 $\mu$ 近似为样本平均数 $\bar{x}, \sigma^2$ 近似为样本方差 $s^2$ .
① 若使 $84.14 \%$ 的产品的质量指标值高于企业制定的合格标准,则合格标准的质量指标值大约为多少?
② 若该企业又生产了这种产品 1000 件,且每件产品相互独立,则这 1000 件产品质量指标值不低于 12.14的件数最有可能是多少?
附:$\sum_{i=1}^7\left( x _{ i }-\overline{ x }\right)^2 h_{ i }=3.46,3.46 \approx \frac{1}{2} \times 2.63^2$ ;若 $X \sim N \left(\mu, \sigma^2\right)$ ,则 $P (\mu-\sigma < X \leqslant \mu+\sigma)=0.6827 ; P (\mu-2 \sigma < X \leqslant \mu +2 \sigma)=0.9545 ; P (\mu-3 \sigma < X \leqslant \mu+3 \sigma)=0.9973$.
$5 G$ 网络是第五代移动通信网络的简称,是新一轮科技革命最具代表性的技术之一. 2020 年初以来,我国 $5 G$网络正在大面积铺开.$A$ 市某调查机构为了解市民对该市 $5 G$ 网络服务质量的满意程度,从使用了 $5 G$ 手机的市民中随机选取了 200 人进行问卷调查,并将这 200 人根据其满意度得分分成以下 6 组:[40,50)、[50,60)、 $[60,70)$ ,...,[90,100],统计结果如图所示:
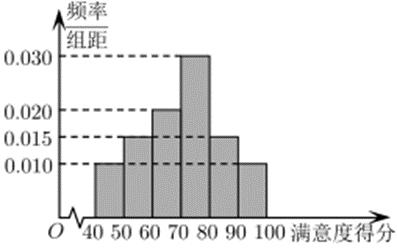
(1)由直方图可认为 $A$ 市市民对 $5 G$ 网络满意度得分 $Z$(单位:分)近似地服从正态分布 $N\left(\mu, \sigma^2\right)$ ,其中 $\mu$ 近似为样本平均数 $\bar{x}, \sigma$ 近似为样本的标准差 $s$ ,并已求得 $s=14.31$ .若 $A$ 市恰有 2 万名 $5 G$ 手机用户,试估计这些 $5 G$ 手机用户中满意度得分位于区间( $41.88,84.81$ ]的人数(每组数据以区间的中点值为代表);
(2)该调查机构为参与本次调查的 $5 G$ 手机用户举行了抽奖活动,每人最多有 3 轮抽奖活动,每一轮抽奖相互独立,中奖率均为 $\frac{1}{3}$ .每一轮抽奖,奖金为 100 元话费且继续参加下一轮抽奖;若未中奖,则抽奖活动结束.现小王参与了此次抽奖活动,求小王所获话费总额 $x$ 的数学期望.
参考数据:若随机变量 $Z$ 服从正态分布 $N\left(\mu, \sigma^2\right)$ ,即 $Z \sim N\left(\mu, \sigma^2\right)$ ,则 $P(\mu-\sigma < Z \leq \mu+\sigma)=0.6827$ , $P(\mu-2 \sigma < Z \leq \mu+2 \sigma)=0.9545$ .
法国数学家庞加莱是个喜欢吃面包的人,他每天都会到同一家面包店购买一个面包。该面包店的面包师声称自己所出售的面包的平均质量是 1000 g ,上下浮动不超过 50 g 。这句话用数学语言来表达就是:每个面包的质量服从期望为 1000 g ,标准差为 50 g 的正态分布.
(1)已知如下结论:若 $X: N\left(\mu, \sigma^2\right)$ ,从 $X$ 的取值中随机抽取 $k\left(k \in N^*, k \geq 2\right)$ 个数据,记这 $k$ 个数据的平均值为 $Y$ ,则随机变量 $Y \sim N\left(\mu, \frac{\sigma^2}{k}\right)$ .利用该结论解决下面问题.
(i)假设面包师的说法是真实的,随机购买 25 个面包,记随机购买 25 个面包的平均值为 $Y$ ,求 $P(Y \leq 980)$ ;
(ii)庞加莱每天都会将买来的面包称重并记录, 25 天后,得到的数据都落在 $(950,1050)$ 上,并经计算 25个面包质量的平均值为 978.72 g 。庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有 6 个面包,其中黑色面包有 2 个;第二箱中共装有 8 个面包,其中黑色面包有 3 个.现随机挑选一箱,然后从该箱中随机取出 2 个面包.求取出黑色面包个数的分布列及数学期望.
附:
① 随机变量 $\eta$ 服从正态分布 $N\left(\mu, \sigma^2\right)$ ,则 $P(\mu-\sigma \leq \eta \leq \mu+\sigma)=0.6827$ ,
$$
P(\mu-2 \sigma \leq \eta \leq \mu+2 \sigma)=0.9545, P(\mu-3 \sigma \leq \eta \leq \mu+3 \sigma)=0.9973 ;
$$
② 通常把发生概率小于 0.05 的事件称为小概率事件,小概率事件基本不会发生.