$5 G$ 网络是第五代移动通信网络的简称，是新一轮科技革命最具代表性的技术之一． 2020 年初以来，我国 $5 G$网络正在大面积铺开．$A$ 市某调查机构为了解市民对该市 $5 G$ 网络服务质量的满意程度，从使用了 $5 G$ 手机的市民中随机选取了 200 人进行问卷调查，并将这 200 人根据其满意度得分分成以下 6 组：［40，50）、［50，60）、 $[60,70)$ ，．．．，［90，100］，统计结果如图所示：

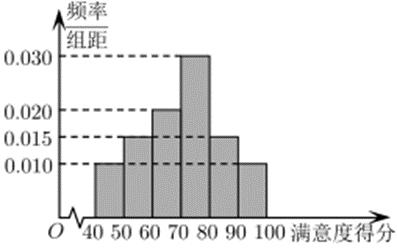
（1）由直方图可认为 $A$ 市市民对 $5 G$ 网络满意度得分 $Z$（单位：分）近似地服从正态分布 $N\left(\mu, \sigma^2\right)$ ，其中 $\mu$ 近似为样本平均数 $\bar{x}, \sigma$ 近似为样本的标准差 $s$ ，并已求得 $s=14.31$ ．若 $A$ 市恰有 2 万名 $5 G$ 手机用户，试估计这些 $5 G$ 手机用户中满意度得分位于区间（ $41.88,84.81$ ］的人数（每组数据以区间的中点值为代表）；
（2）该调查机构为参与本次调查的 $5 G$ 手机用户举行了抽奖活动，每人最多有 3 轮抽奖活动，每一轮抽奖相互独立，中奖率均为 $\frac{1}{3}$ ．每一轮抽奖，奖金为 100 元话费且继续参加下一轮抽奖；若未中奖，则抽奖活动结束．现小王参与了此次抽奖活动，求小王所获话费总额 $x$ 的数学期望．

参考数据：若随机变量 $Z$ 服从正态分布 $N\left(\mu, \sigma^2\right)$ ，即 $Z \sim N\left(\mu, \sigma^2\right)$ ，则 $P(\mu-\sigma < Z \leq \mu+\sigma)=0.6827$ ， $P(\mu-2 \sigma < Z \leq \mu+2 \sigma)=0.9545$ ．