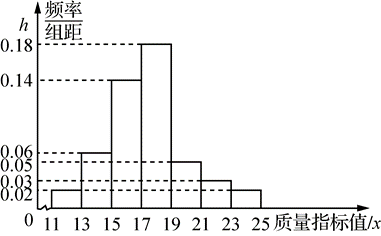
从某企业的某种产品中抽取 500 件，测量这些产品的一项质量指标值，由测量结果得如下频率直方图：
（1）求这 500 件产品质量指标值的样本平均数 $\overline{ x }$ 和样本方差 $s ^2$（同一组数据用该区间的中点值作代表，记作 $x _{ i }, i =1,2, \cdots, 7$ ）；
（2）由频率直方图可以认为，这种产品的质量指标值 X 服从正态分布 $N \left(\mu, \sigma^2\right)$ ，其中 $\mu$ 近似为样本平均数 $\bar{x}, \sigma^2$ 近似为样本方差 $s^2$ ．
① 若使 $84.14 \%$ 的产品的质量指标值高于企业制定的合格标准，则合格标准的质量指标值大约为多少？
② 若该企业又生产了这种产品 1000 件，且每件产品相互独立，则这 1000 件产品质量指标值不低于 12.14的件数最有可能是多少？

附：$\sum_{i=1}^7\left( x _{ i }-\overline{ x }\right)^2 h_{ i }=3.46,3.46 \approx \frac{1}{2} \times 2.63^2$ ；若 $X \sim N \left(\mu, \sigma^2\right)$ ，则 $P (\mu-\sigma < X \leqslant \mu+\sigma)=0.6827 ; P (\mu-2 \sigma < X \leqslant \mu +2 \sigma)=0.9545 ; P (\mu-3 \sigma < X \leqslant \mu+3 \sigma)=0.9973$.