单选题 (共 6 题 ),每题只有一个选项正确
在 $\triangle AB C$ 中,点 $D$ 在边 $A B$ 上,$B D=2 D A$ .记 $\overrightarrow{C A}=\vec{m}, \overrightarrow{C D}=\vec{n}$ ,则 $\overrightarrow{C B}=$
$\text{A.}$ $3 \vec{m}-2 \vec{n}$
$\text{B.}$ $-2 \vec{m}+3 \vec{n}$
$\text{C.}$ $3 \vec{m}+2 \vec{n}$
$\text{D.}$ $2 \vec{m}+3 \vec{n}$
在 $\triangle A B C$ 中,$D$ 是 $A B$ 边上的中点,则 $\overrightarrow{C B}=$
$\text{A.}$ $2 \overrightarrow{C D}+\overrightarrow{C A}$
$\text{B.}$ $\overrightarrow{C D}-2 \overrightarrow{C A}$
$\text{C.}$ $2 \overrightarrow{C D}-\overrightarrow{C A}$
$\text{D.}$ $\overrightarrow{C D}+2 \overrightarrow{C A}$
已知 $\overrightarrow{M P}=4 \mathrm{e}_{1}+2 \mathrm{e}_{2}, \overrightarrow{P Q}=2 \mathrm{e}_{1}+t \mathrm{e}_{2}$ ,若 $M 、 P 、 Q$ 三点共线,则 $t=()$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 4
$\text{D.}$ -1
已知 $\overrightarrow{A B}=\boldsymbol{a}+5 \boldsymbol{b}, \overrightarrow{B C}=-3 \boldsymbol{a}+6 \boldsymbol{b}, \overrightarrow{C D}=4 \boldsymbol{a}-\boldsymbol{b}$ ,则
$\text{A.}$ $A, B, D$ 三点共线
$\text{B.}$ $A, B, C$ 三点共线
$\text{C.}$ $B, C, D$ 三点共线
$\text{D.}$ $A, C, D$ 三点共线
给出下列命题,正确的有( )
$\text{A.}$ 若两个向量相等,则它们的起点相同,终点相同
$\text{B.}$ 若 $A, B, C, D$ 是不共线的四点,且 $\overrightarrow{A B}=\overrightarrow{D C}$ ,则四边形 $A B C D$ 为平行四边形
$\text{C.}$ $\boldsymbol{a}=\boldsymbol{b}$ 的充要条件是 $|\boldsymbol{a}|=|\boldsymbol{b}|$ 且 $\boldsymbol{a} / / \boldsymbol{b}$
$\text{D.}$ 已知 $\lambda, \mu$ 为实数,若 $\lambda \boldsymbol{a}=\mu \boldsymbol{b}$ ,则 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 共线
如图在梯形 $ A B C D$ 中,$B C=2 A D, D E=E C$ ,设 $\overrightarrow{B A}=\vec{a}, \overrightarrow{B C}=$
$\vec{b}$ ,则 $\overrightarrow{B E}=$
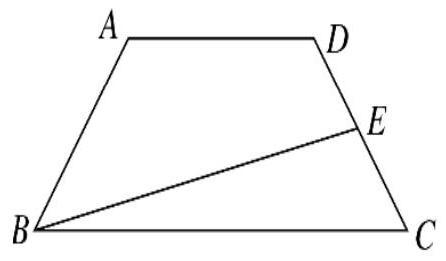
$\text{A.}$ $\frac{1}{2} \vec{a}+\frac{1}{4} \vec{b}$
$\text{B.}$ $\frac{1}{3} \vec{a}+\frac{5}{6} \vec{b}$
$\text{C.}$ $\frac{2}{3} \vec{a}+\frac{2}{3} \vec{b}$
$\text{D.}$ $\frac{1}{2} \vec{a}+\frac{3}{4} \vec{b}$
多选题 (共 1 题 ),每题有多个选项正确
如图,在四边形 $ A B C D$ 中,$A B / / C D, A B \perp A D, A B=2 A D=2 D C, E$ 为 $B C$ 边上一点,且 $\overrightarrow{B C}=3 \overrightarrow{E C}, F$ 为 $A E$的中点,则
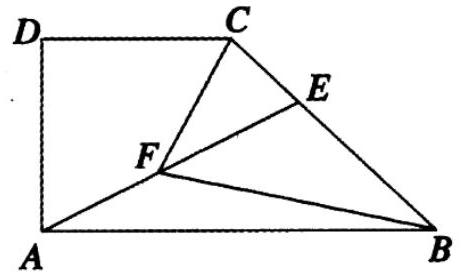
$\text{A.}$ $\overrightarrow{B C}=-\frac{1}{2} \overrightarrow{A B}+\overrightarrow{A D}$
$\text{B.}$ $\overrightarrow{A F}=\frac{1}{3} \overrightarrow{A B}+\frac{1}{3} \overrightarrow{A D}$
$\text{C.}$ $\overrightarrow{B F}=-\frac{2}{3} \overrightarrow{A B}+\frac{1}{3} \overrightarrow{A D}$
$\text{D.}$ $\overrightarrow{C F}=\frac{1}{6} \overrightarrow{A B}-\frac{2}{3} \overrightarrow{A D}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
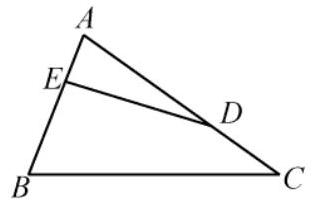
如图,在 $\triangle A B C$ 中,$\frac{C D}{D A}=\frac{A E}{E B}=\frac{1}{2}$ ,若 $\overrightarrow{D E}=\lambda \overrightarrow{C A}+\mu \overrightarrow{C B}$ ,则 $\lambda+\mu=$ $\qquad$ .
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设两个非零向量 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 不共线.
(1)若 $\overrightarrow{A B}=\boldsymbol{a}+\boldsymbol{b}, \overrightarrow{B C}=2 \boldsymbol{a}+8 \boldsymbol{b}, \overrightarrow{C D}=3(\boldsymbol{a}-\boldsymbol{b})$ ,求证:$A, B, D$ 三点共线;
(2)试确定实数 $k$ ,使 $k \boldsymbol{a}+\boldsymbol{b}$ 和 $\boldsymbol{a}+k \boldsymbol{b}$ 同向.
如图,在 $\triangle A B C$ 中,$D$ 是 $B C$ 上靠近点 $B$ 的四等分点,$E, F$ 分别为 $A C, A D$ 的三等分点,且分别靠近 $A, D$ 两点,设 $\overrightarrow{A B}=\boldsymbol{a}, \overrightarrow{A C}=\boldsymbol{b}$ .
(1)试用 $\boldsymbol{a}, \boldsymbol{b}$ 表示 $\overrightarrow{B C}, \overrightarrow{A D}, \overrightarrow{B E}$ ;
(2)证明:$B, E, F$ 三点共线.
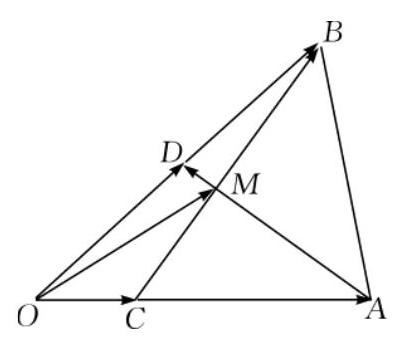
如图,在 $\triangle \mathrm{ABO}$ 中, $\overrightarrow{\mathrm{OC}}=\frac{1}{4} \overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OD}}=\frac{1}{2} \overrightarrow{\mathrm{OB}}, \mathrm{AD}$ 与 BC 相交于点 M ,设 $\overrightarrow{\mathrm{OA}}=\mathrm{a}, \overrightarrow{\mathrm{OB}}=\mathrm{b}$ .试用 a 和 b 表示 $\overrightarrow{O M}$ .