单选题 (共 21 题 ),每题只有一个选项正确
若集合 $M=\left\{x \mid 2^x>4\right\}, N=\left\{x \mid \log _3 x \leqslant 1\right\}$ ,则 $M \cup N =$( )
$\text{A.}$ $\{x \mid 2 < x \leqslant 3\}$
$\text{B.}$ $\{x \mid x>0\}$
$\text{C.}$ $\{x \mid 0 < x < 2$ 或 $x>2$ )
$\text{D.}$ $R$
已知集合 $A=\{-1,1,2\}, B=\{x \mid x-1 \geqslant 0\}$ ,则 $A \cup B=(\quad)$
$\text{A.}$ $\{1,2\}$
$\text{B.}$ $[1,+\infty)$
$\text{C.}$ $[-1,+\infty)$
$\text{D.}$ $\{-1\} \cup[1,+\infty)$
已知 $A=\left\{y \mid y=a^x(a>0, a \neq 1)\right\}, B=\left\{x \mid x^2>x\right\}$ ,则 $A \cap B=$( )
$\text{A.}$ $(0,+\infty)$
$\text{B.}$ $(1,+\infty)$
$\text{C.}$ $(-\infty, 0)$
$\text{D.}$ $(-\infty, 0) \cup(1,+\infty)$
已知集合 $A=\{x| | x \mid < 4, x \in Z \}, B=\left\{y \mid y^2>4\right\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\{-4,-3,3,4\}$
$\text{B.}$ $\{-3,3\}$
$\text{C.}$ $\{3\}$
$\text{D.}$ $\emptyset$
若集合 $A=\{0,1,3,4,7\}, B=\{-2,0,3,4\}$ ,则 $A \cap B$ 中元素的个数为( )
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 1
设全集 $U=\left\{x \in Z \mid x^2 \leqslant 2 x+3\right\}$ ,集合 $A=\{0,1,2\}$ ,则 $C_U A=(\quad)$
$\text{A.}$ $\{0,3\}$
$\text{B.}$ $\{-1,0\}$
$\text{C.}$ $\{-1,3\}$
$\text{D.}$ $\{-1,0,3\}$
设全集 $U=\{1,2,3,4,5,6\}$ ,集合 $A=\left\{x \mid x^2-6 x+8 \leqslant 0, x \in Z\right\}$ ,则 $C_U A=(\quad)$
$\text{A.}$ $\{2,3,4\}$
$\text{B.}$ $\{1,5,6\}$
$\text{C.}$ $\{4,5,6\}$
$\text{D.}$ $\{1,2,3\}$
全集 $U=\{-3,-2,-1,0,1,2,3,4,5\}$ ,集合 $A=\left\{x \mid x^2 < 5, x \in Z\right\}$ ,则 $C_U A=()$
$\text{A.}$ $C_U A=\{-3,-2,2,3,4,5\}$
$\text{B.}$ $C_U A=\{-3,3,4,5\}$
$\text{C.}$ $C_U A=\{3,4,5\}$
$\text{D.}$ $C_u A=\{-2,-1,0,1,2\}$
设集合 $A=\{4,5,7,9\}, B=\{3,4,7,8,9\}$ ,全集 $U=A \cup B$ ,则集合 $C_U(A \cap B)$ 中的元素共有
$\text{A.}$ 3 个
$\text{B.}$ 4 个
$\text{C.}$ 5 个
$\text{D.}$ 6 个
已知全集 $U=\{-2,-1,0,1,2,3\}, M=\{x \mid x>0\}, N=\{x \in Z \mid-2 < x < 2\}$ ,则 $M \cap\left(C_U N\right)=$
$\text{A.}$ $\{3\}$
$\text{B.}$ $\{2,3\}$
$\text{C.}$ $\{1,2,3\}$
$\text{D.}$ $\{-2,2,3\}$
已知全集 $U=\{0,1,2,3,4,5\}$ ,集合 $A=\{0,1,3\}$ ,集合 $B=\{2,3,4\}$ ,则 $\left(C_U A\right) \cap B=()$
$\text{A.}$ $\{2,4\}$
$\text{B.}$ $\{3,4\}$
$\text{C.}$ $\{2,3\}$
$\text{D.}$ $\{4\}$
用 $C(A)$ 表非空集合 $A$ 中元素的个数,定义 $A * B=\left\{\begin{array}{ll}C(A)-C(B), & C(A) \geqslant C(B) \\ C(B)-C(A), & C(A) < C(B)\end{array}\right.$ ,若 $A=\{1\}, B=$ $\left\{x \mid x\left(x^2+a x+2\right)=0\right\}$ ,且 $A^* B=1$ ,设实数 $a$ 的所有可能取值构成集合 $S$ ,则 $C(S)= $
$\text{A.}$ 4
$\text{B.}$ 3
$\text{C.}$ 2
$\text{D.}$ 9
设集合 $M, ~ P \neq \emptyset$ ,定义集合 $M-P=\{x \mid x \in M, x \notin P\}$ ,则集合 $M-(M-P)$ 是( )
$\text{A.}$ $P$
$\text{B.}$ $M$
$\text{C.}$ $M \cup P$
$\text{D.}$ $M \cap P$
定义集合 $A, B$ 的一种运算:$A^* B=\left\{x \mid x=x_1+x_2, x_1 \in A, x_2 \in B\right\}$ ,若 $A=\{1,2,3\}, B=\{1,2\}$ ,则 $A^* B$ 的元素个数为
$\text{A.}$ 6 个
$\text{B.}$ 5 个
$\text{C.}$ 4 个
$\text{D.}$ 3 个
集合论是德国数学家康托尔(G.Cantor)于 19 世纪末创立的.在他的集合理论中,用 card(A)表示有限集合 $A$ 中元素的个数,例如:$A=\{a, b, c\}$ ,则 $\operatorname{card}(A)=3$ .对于任意两个有限集合 $A, B$ ,有 $\operatorname{card}$ $(A \cup B)=\operatorname{card}(A)+\operatorname{card}(B)-\operatorname{card}(A \cap B)$ .某校举办运动会,高一(1)班参加田赛的学生有 15 人,参加径赛的学生有 13 人,两项都参加的有 5 人,那么高一(1)班参加本次运动会的人数共有( )

$\text{A.}$ 28
$\text{B.}$ 23
$\text{C.}$ 18
$\text{D.}$ 16
若全集 $U=R$ ,集合 $A=\{0,1,2,3,4,5,6\}, B=\{x \mid x < 3\}$ ,则图中阴影部分表示的集合为
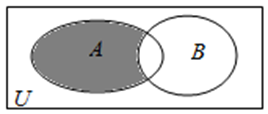
$\text{A.}$ $\{3,4,5,6\}$
$\text{B.}$ $\{0,1,2\}$
$\text{C.}$ $\{0,1,2,3\}$
$\text{D.}$ $\{4,5,6\}$
如图,$U$ 是全集,$M, N, P$ 是 $U$ 的三个子集,则阴影部分所表示的集合是
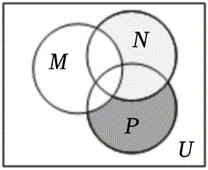
$\text{A.}$ $\left(C_U M\right) \cap\left(C_U N\right) \cap P$
$\text{B.}$ $(C \cup M) \cap P$
$\text{C.}$ $C_U(M \cap N) \cap P$
$\text{D.}$ $C _{\cup}(M \cup N ) \cup P$
设全集 $U=\{-2,-1,0,1,2\}$ ,集合 $A=\{1,-1,0\}, B=\{-1,2\}$ ,则 $A \cup C_U B=(\quad)$
$\text{A.}$ $\{0,1\}$
$\text{B.}$ $\{-2,0,1\}$
$\text{C.}$ $\{-1,0,1\}$
$\text{D.}$ $\{-2,-1,0,1\}$
已知集合 $A=\left\{x \mid x^2-x-6 < 0\right\}, B=\{x \mid 2 x+3>0\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\left(-2,-\frac{3}{2}\right)$
$\text{B.}$ $\left(\frac{3}{2}, 3\right)$
$\text{C.}$ $\left(-\frac{3}{2}, 3\right)$
$\text{D.}$ $\left(-\frac{3}{2}, 2\right)$
若 $M, N$ 是 $U$ 的非空子集,$M \cap N =M$ ,则
$\text{A.}$ $M \subseteq N$
$\text{B.}$ $N \subseteq M$
$\text{C.}$ $C_U M=N$
$\text{D.}$ $C_u N=M$
已知集合 $A=\{x \mid \ln (x-2) < 0\}, B=\{x \mid 5-2 x>0\}$ ,则 $A \cap B=(\quad)$
$\text{A.}$ $\left\{x \left\lvert\, 2 < x < \frac{5}{2}\right.\right\}$
$\text{B.}$ $\left\{x \left\lvert\, \frac{5}{2} < x < 3\right.\right\}$
$\text{C.}$ $\left\{x \left\lvert\, 1 < x < \frac{5}{2}\right.\right\}$
$\text{D.}$ $\{x \mid 1 < x < 2\}$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知集合 $A=\left\{2,3, a^2+4 a+2\right\}, B=\left\{0,7, a^2+4 a-2,2-a\right\}$ ,且 $A \cap B=\{3,7\}$ ,求集合 $B$ .
已知集合 $A=\{x \mid-2 \leqslant x \leqslant 5\}, B=\{x \mid m+1 \leqslant x \leqslant 2 m-1\}$ ,若 $B \subseteq A$ ,求实数 $m$ 的取值范围.