甲，乙两个箱子装有大小及外观相同的小球，甲箱中有 5 个白球和 3个黑球，乙箱中有 4 个白球和 3 个黑球。
（1）若从甲箱中任取 2 个小球，求这 2 个小球同色的概率；
（2）若先从甲箱中任取 2 个小球放入乙箱中，然后再从乙箱中任取 1 个小球，求从乙箱中取出的球是白球的概率．

已知函数 $f(x)=x^2+x$ ．数列 $\left\{x_n\right\}\left(x_n < -1\right)$ 的首项 $x_1=\frac{e}{1-e}$ ．以后各项按如下方式取定：记曲线 $y=f(x)$ 在 $\left(x_n, f\left(x_n\right)\right)$ 处的切线为 $l_n$ ，若 $f^{\prime}\left(x_n\right) \neq 0$ ，则记 $l_n$与 $x$ 轴交点的横坐标是 $x_{n+1}$ ．
（1）证明：数列 $\left\{\ln \frac{x_n}{x_n+1}\right\}$ 为等比数列；
（2）设 $a_n=\ln \frac{x_n}{x_n+1}$ ，求数列 $\left\{n \cdot a_n\right\}$ 的前 $n$ 项和 $S_n$ ．

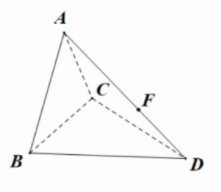
如图，三棱锥 $A-B C D$ 中，$B C=C D=B D=2, A B=A C=\sqrt{2}$ ．异面直线 $A C$ 和 $B D$ 所成角的余弦值为 $\frac{\sqrt{2}}{4}$ ，点 $F$ 是线段 $A D$ 上的一个动点．
（1）证明：平面 $A B C \perp$ 平面 $B C D$ ；
（2）若二面角 $B-C F-D$ 的正弦值为 $\frac{\sqrt{33}}{7}$ ，求 $D F$ ．

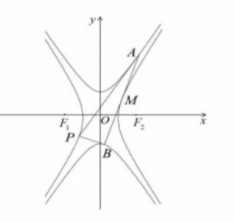
如图，双曲线 $C_1: x^2-\frac{y^2}{3}=1$ 的左右焦点分别为 $F_1, F_2$ ，双曲线 $C_2: \frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0, \quad b>0)$ 与 $C_1$ 有相同的渐近线和焦距．过 $C_1$ 上一点 $P\left(x_0, y_0\right)$ 作 $C_2$的两条切线，切点分别为 $A, B, A$ 在 $x$ 轴上方，连接 AB 交 $C_1$ 于点 $M$ ．
（注：过曲线 $\frac{x^2}{m}+\frac{y^2}{n}=1$ 外一点 $\left(x^{\prime}, y^{\prime}\right)$ 作曲线的两条切线，则两切点所在直线方程为 $\frac{x^{\prime} x}{m}+\frac{y^{\prime} y}{n}=1$ ）
（1）求双曲线 $C_2$ 的方程；
（2）证明：直线 $A B$ 与 $C_1$ 切于点 $M$ ，且 $|A M|=|B M|$ ；
（3）当点 $P\left(x_0, y_0\right)$ 在第三象限，且 $P M / / B F_2$ 时，求 $S_{\triangle M F_1 F_2}$ 的值．

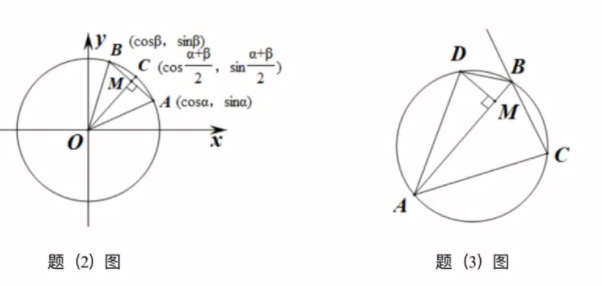
（1）证明： $\sin a+\sin \beta=2 \sin \frac{a+\beta}{2} \cdot \cos \frac{a-\beta}{2}$ ；
（2）当 $0 < a < \beta < \frac{\pi}{2}$ 时，利用所给图形证明（1）中等式；
（3）如图，$\triangle A B C$ 的外接圆半径为 $1, A B>A C, \angle A B C$ 的一个外角的角平分线交外接圆于点 $D$ ，过 $D$ 作 $D M \perp A B$ 于点 $M$ ，利用（1）中等式，证明： $2 A M=B A+B C$ ．