（1）证明： $\sin a+\sin \beta=2 \sin \frac{a+\beta}{2} \cdot \cos \frac{a-\beta}{2}$ ；
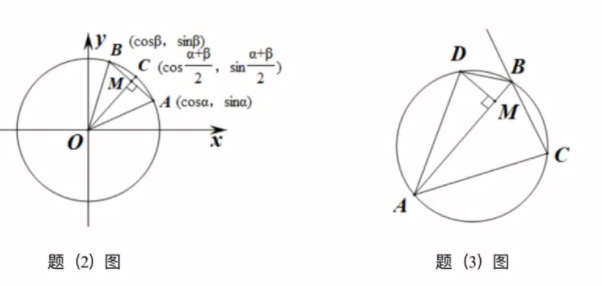
（2）当 $0 < a < \beta < \frac{\pi}{2}$ 时，利用所给图形证明（1）中等式；
（3）如图，$\triangle A B C$ 的外接圆半径为 $1, A B>A C, \angle A B C$ 的一个外角的角平分线交外接圆于点 $D$ ，过 $D$ 作 $D M \perp A B$ 于点 $M$ ，利用（1）中等式，证明： $2 A M=B A+B C$ ．