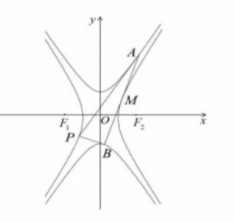
如图，双曲线 $C_1: x^2-\frac{y^2}{3}=1$ 的左右焦点分别为 $F_1, F_2$ ，双曲线 $C_2: \frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0, \quad b>0)$ 与 $C_1$ 有相同的渐近线和焦距．过 $C_1$ 上一点 $P\left(x_0, y_0\right)$ 作 $C_2$的两条切线，切点分别为 $A, B, A$ 在 $x$ 轴上方，连接 AB 交 $C_1$ 于点 $M$ ．
（注：过曲线 $\frac{x^2}{m}+\frac{y^2}{n}=1$ 外一点 $\left(x^{\prime}, y^{\prime}\right)$ 作曲线的两条切线，则两切点所在直线方程为 $\frac{x^{\prime} x}{m}+\frac{y^{\prime} y}{n}=1$ ）
（1）求双曲线 $C_2$ 的方程；
（2）证明：直线 $A B$ 与 $C_1$ 切于点 $M$ ，且 $|A M|=|B M|$ ；
（3）当点 $P\left(x_0, y_0\right)$ 在第三象限，且 $P M / / B F_2$ 时，求 $S_{\triangle M F_1 F_2}$ 的值．