单选题 (共 10 题 ),每题只有一个选项正确
设函数 $f(x)=\left\{\begin{array}{ll}1+\sin \frac{\pi}{2} x, & x \leqslant 1, \\ 2-\sqrt{x-1}, & x>1 .\end{array}\right.$ 对 $f(x)$ 给出两个命题:①点 $x=1$ 是 $f(x)$ 的一个极 值点; ②点 $(1,2)$ 是曲线 $y=f(x)$ 的一个拐点. 则
$\text{A.}$ ①和 ② 都正确.
$\text{B.}$ ①正确,但② 不正确.
$\text{C.}$ ① 不正确, 但② 正确.
$\text{D.}$ ①和② 都不正确.
设函数 $f(x)$ 在闭区间 $[0,2]$ 上二阶可导, 且 $f^{\prime \prime}(x)>0$, 又 $f(0)=2 f(1)=f(2)=2$, 则
$\text{A.}$ $1 < \int_0^2 f(x) \mathrm{d} x < 2$.
$\text{B.}$ $\frac{3}{2} < \int_0^2 f(x) \mathrm{d} x < \frac{5}{2}$.
$\text{C.}$ $2 < \int_0^2 f(x) \mathrm{d} x < 3$.
$\text{D.}$ $3 < \int_0^2 f(x) \mathrm{d} x < 4$.
设函数 $f(x)=\iint_{u^2+v^2 \leqslant x^2} \arctan \left(1+\sqrt{u^2+v^2}\right) \mathrm{d} u \mathrm{~d} v(x>0)$, 则 $\lim _{x \rightarrow 0^{+}} \frac{f(x)}{\mathrm{e}^{-2 x}-1+2 x}=$
$\text{A.}$ $-\frac{\pi^2}{8}$.
$\text{B.}$ $-\frac{\pi^2}{4}$.
$\text{C.}$ $\frac{\pi^2}{4}$.
$\text{D.}$ $\frac{\pi^2}{8}$.
设 $f(x)=\left\{\begin{array}{ll}x+1, & 0 \leqslant x \leqslant \pi, \\ 0, & -\pi \leqslant x < 0,\end{array} S(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left(a_n \cos n x+b_n \sin n x\right)\right.$ 是 $f(x)$ 以 $2 \pi$ 为周 期的傅里叶级数, 则 $\sum_{n=1}^{\infty} a_n=$
$\text{A.}$ $-\frac{\pi}{4}$.
$\text{B.}$ $\frac{\pi}{4}$.
$\text{C.}$ $-\frac{\pi}{2}$.
$\text{D.}$ $\frac{\pi}{2}$.
设 $f(x)=\left|\begin{array}{ccccc}x+1 & 2 & 3 & \cdots & n \\ 1 & x+2 & 3 & \cdots & n \\ 1 & 2 & x+3 & \cdots & n \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & 2 & 3 & \cdots & x+n\end{array}\right|$
, 则 $f^{(n-1)}(0)=$
$\text{A.}$ $\frac{1}{2} n(n+1)$.
$\text{B.}$ $\frac{1}{2}(n+1) !$.
$\text{C.}$ $n !$.
$\text{D.}$ $(n+1)$ !.
设 $\boldsymbol{A}$ 是 $m \times n$ 矩阵, $m < n, r(\boldsymbol{A})=m$, 以下选项中错误的是
$\text{A.}$ 存在 $n$ 阶可逆矩阵 $Q$, 使得 $A Q=\left(\boldsymbol{E}_m \mid \boldsymbol{O}\right)$.
$\text{B.}$ 存在 $m$ 阶可逆矩阵 $\boldsymbol{P}$, 使得 $\boldsymbol{P A}=\left(\boldsymbol{E}_m \boldsymbol{O}\right)$.
$\text{C.}$ 齐次线性方程组 $A x=0$ 有零解.
$\text{D.}$ 非齐次线性方程组 $\boldsymbol{A x}=\boldsymbol{b}$ 有无穷多解.
设 $\boldsymbol{A}$ 是 3 阶实矩阵, 则 “ $\boldsymbol{A}$ 是实对称矩阵” 是“ $\boldsymbol{A}$ 有 3 个相互正交的特征向量” 的
$\text{A.}$ 充分非必要条件.
$\text{B.}$ 必要非充分条件.
$\text{C.}$ 充分必要条件.
$\text{D.}$ 既非充分也非必要条件.
设某人每次射击命中的概率都为 $p(0 < p < 1)$, 则他第 8 次射击恰好是第 4 次命中的概率为
$\text{A.}$ $35 p^3(1-p)^4$.
$\text{B.}$ $35 p^4(1-p)^3$.
$\text{C.}$ $35 p^4(1-p)^4$.
$\text{D.}$ $35 p^5(1-p)^3$.
设 $X, Y$ 是两个随机变量, $E(X)=2, E(Y)=-1, D(X)=9, D(Y)=16$, 且 $X, Y$ 的相关系数 为 $\rho=-\frac{1}{2}$, 已知由切比雪夫不等式可得 $P\{|X+Y-1| < 10\} \geqslant k$, 则 $k$ 的值等于
$\text{A.}$ $\frac{9}{16}$.
$\text{B.}$ $\frac{3}{4}$.
$\text{C.}$ $\frac{21}{25}$.
$\text{D.}$ $\frac{87}{100}$.
设总体 $X$ 的概率分布如下
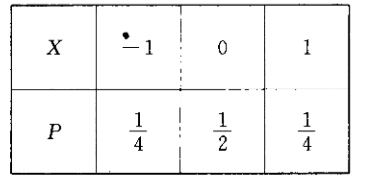
从总体中抽取 $n$ 个简单随机样本, $N_1$ 表示 $n$ 个样本中取到 -1 的个数, $N_2$ 表示 $n$ 个样本中取 到 0 的个数, $N_3$ 表示 $n$ 个样本中取到 1 的个数, 则 $N_1$ 与 $N_2$ 的相关系数为
$\text{A.}$ $-\frac{\sqrt{3}}{3}$.
$\text{B.}$ $\frac{\sqrt{3}}{3}$.
$\text{C.}$ $-1$
$\text{D.}$ $1$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若四阶常系数齐次线性微分方程有一个解为 $y=x \mathrm{e}^x \cos 2 x$, 则该方程的通解为
设 $f(x)$ 为 $[0,3]$ 上的非负连续函数, 且满足 $f(x) \int_1^2 f(x t-x) \mathrm{d} t=2 x^2, x \in[0,3]$, 则 $f(x)$ 在 区间 $[1,3]$ 上的平均值为
设函数 $f(x, y)$ 可微, $f(x, y)$ 在点 $P_0(1,1)$ 处指向点 $P_1(-7,16)$ 的方向导数等于 $\frac{13}{17}$,指向点 $P_2(6,-11)$ 的方向导数等于 $-\frac{16}{13}$, 则 $f(x, y)$ 在点 $P_0(1,1)$ 处的最大方向导数为
一质点在变力 $\boldsymbol{F}=\left(1-x^2\right) y^3 \boldsymbol{i}-x^3\left(1+y^2\right) \boldsymbol{j}$ 的作用下从圆周 $L: x^2+y^2=1$ 上的任一点出 发沿逆时针方向运动一周, 则变力 $\boldsymbol{F}$ 对质点所做的功等于
设 $\boldsymbol{A}$ 为 4 阶矩阵, $(\boldsymbol{A}-2 \boldsymbol{E}) \boldsymbol{x}=\mathbf{0}$ 的基础解系中只有 2 个解向量, $(\boldsymbol{A}+\boldsymbol{E}) \boldsymbol{x}=$ 0 的基础解系中只有 1 个解向量, 则 $r\left(\boldsymbol{A}^2-\boldsymbol{A}-2 \boldsymbol{E}\right)=$
已知 $P(\bar{B} \mid A)=\frac{1}{3}, P(B \mid \bar{A})=\frac{4}{7}, P(A B)=\frac{1}{5}$, 则 $P(\bar{A} \bar{B})=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设可导函数 $f(x)$ 满足 $\int x^3 f^{\prime}(x) \mathrm{d} x=x^2 \cos x-4 x \sin x-6 \cos x+C$, 且 $f(2 \pi)=\frac{1}{2 \pi}$, 求
$$
\int f(x) d x .
$$
设 $a, b$ 满足条件 $a \geqslant 0, b \leqslant 0$ 及 $\int_a^b|x| \mathrm{d} x=-\frac{1}{2}$, 求直线 $y=a x$ 与抛物线 $y=x^2+b x$ 所围 成区域的面积的最大值与最小值.
设 $F(x)$ 是 $f(x)$ 的一个原函数, 且 $F(0)=1, F(x) f(x)=\cos 2 x, a_n=\int_0^{n \pi}|f(x)| \mathrm{d} x(n-1$, $2, \cdots)$.
(1) 求 $a_n$;
(2) 求幂级数 $\sum_{n=2}^{\infty} \frac{a_n}{n^2-1} x^n$ 的收敛域与和函数.
设空间曲线 $L:\left\{\begin{array}{l}z=x^2+2 y^2, \\ z=6-2 x^2-y^2,\end{array}\right.$ 从 $z$ 轴正向往负向看为逆时针方向, 计算曲线积分
$$
I=\oint_L\left(z^2-y\right) \mathrm{d} x+\left(x^2-z\right) \mathrm{d} y+\left(x-y^2\right) \mathrm{d} z
$$
设 $\boldsymbol{A}$ 是 3 阶矩阵, $\lambda_1, \lambda_2, \lambda_3$ 是 $\boldsymbol{A}$ 的 3 个不同特征值, 对应的特征向量分别为 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3$, 令 $\boldsymbol{\beta}=$ $\boldsymbol{\alpha}_1+\boldsymbol{\alpha}_2+\boldsymbol{\alpha}_3$.
(1) 证明 $\boldsymbol{\beta}=\boldsymbol{\alpha}_1+\boldsymbol{\alpha}_2+\boldsymbol{\alpha}_3$ 不是 $\boldsymbol{A}$ 的特征向量;
(2)证明 $\boldsymbol{\beta}, \boldsymbol{A} \boldsymbol{\beta}, \boldsymbol{A}^2 \boldsymbol{\beta}$ 线性无关;
(3) 若 $\boldsymbol{A}^3 \boldsymbol{\beta}=2 \boldsymbol{A} \boldsymbol{\beta}$, 求 $\boldsymbol{A}$ 的特征值;
(4) 在(3)的基础上证明 $\boldsymbol{A} \boldsymbol{\beta}$ 和 $\boldsymbol{A}^2 \boldsymbol{\beta}$ 是方程组
$$
\left(\boldsymbol{A}^2-2 \boldsymbol{E}\right) \boldsymbol{x}=\mathbf{0}
$$
的基础解系.
设总体 $X$ 的概率密度
$$
f(x ; \theta)= \begin{cases}1, & \theta-\frac{1}{2} \leqslant x \leqslant \theta+\frac{1}{2}, \\ 0, & \text { 其他, }\end{cases}
$$
其中 $-\infty < \theta < +\infty . X_1, X_2, \cdots, X_n$ 为取自总体 $X$ 的简单随机样本, 并记
$$
X_{(1)}=\min \left\{X_1, X_2, \cdots, X_n\right\}, X_{(n)}=\max \left\{X_1, X_2, \cdots, X_n\right\} .
$$
(1) 求参数 $\theta$ 的矩估计量 $\hat{\theta}_M$ 和最大似然估计量 $\hat{\theta}_L$;
(2) 判断 $\frac{X_{(1)}+X_{(n)}}{2}$ 是否为 $\theta$ 的无偏估计量, 并说明理由.