单选题 （共 10 题 ），每题只有一个选项正确
围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史，下列图案属于轴对称的是
$\text{A.}$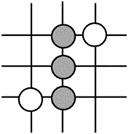 
$\text{B.}$ 
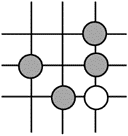$\text{C.}$ 
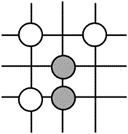$\text{D.}$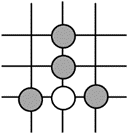 
袁枚的一首诗《苔》中的诗句：＂白日不到处，青春恰自来．苔花如米小，也学牡丹开．＂若诗中苔花的花粉直径约为 0.00000805 m ，则数据 0.00000805 用科学记数法表示为（ ）
$\text{A.}$ $8.05 \times 10^5$
$\text{B.}$ $8.05 \times 10^6$
$\text{C.}$ $8.05 \times 10^{-5}$
$\text{D.}$ $8.05 \times 10^{-6}$
下列二次根式中，属于最简二次根式的是
$\text{A.}$ $\sqrt{\frac{1}{6}}$
$\text{B.}$ $\sqrt{16}$
$\text{C.}$ $\sqrt{6}$
$\text{D.}$ $\sqrt{0.6}$
下列运算错误的是
$\text{A.}$ $a \cdot a^3=a^4$
$\text{B.}$ $a^8 \div a^2=a^6$
$\text{C.}$ $\left(-a^2\right)^3=a^6$
$\text{D.}$ $(-3 a)^2=9 a^2$
下列多边形中，内角和等于360度 的是
$\text{A.}$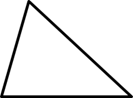 
$\text{B.}$ 
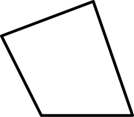$\text{C.}$ 
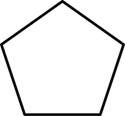$\text{D.}$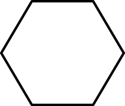 
若 $\frac{a}{b}=M(a \neq b)$ ，则 $M$ 可以是
$\text{A.}$ $\frac{a-2}{b-2}$
$\text{B.}$ $\frac{a+2}{b+2}$
$\text{C.}$ $\frac{-a}{-b}$
$\text{D.}$ $\frac{a^2}{b^2}$
如图，在 $\triangle A B C$ 中，$A B$ 的垂直平分线分别交 $A B 、 B C$ 于点 $D 、 E$ ，连接 $A E$ ，若 $A E=2, E C=1$ ，则 $B C$ 的长是
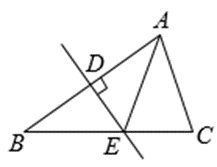
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
如图，边长为 $(m+3)$ 的正方形纸片剪出一个边长为 $m$ 的正方形之后，剩余部分可剪拼成一个矩形（不重叠无缝隙），若拼成的矩形一边长为 3 ，则另一边长是
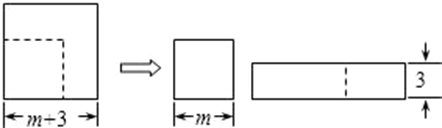
$\text{A.}$ $m+3$
$\text{B.}$ $m+6$
$\text{C.}$ $2 m+3$
$\text{D.}$ $2 m+6$
如在框中解分式方程的4个步骤中，其中根据等式基本性质的有
$\text{A.}$ ①②
$\text{B.}$ ①③
$\text{C.}$ ②④
$\text{D.}$ ③④
如表描述了分式 $\frac{x-m}{x-n}$ 的部分信息：
其中 $x_1 < x_2 < 0 < x_3, y_2 < 0$ ，则下列说法正确的是
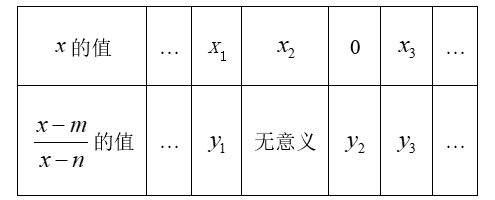
$\text{A.}$ $0 < n < m$
$\text{B.}$ $n < m < 0$
$\text{C.}$ $n < 0 < m$
$\text{D.}$ $m < 0 < n$
填空题 （共 6 题 ），请把答案直接填写在答题纸上
式子 $\sqrt{x-3}$ 在实数范围内有意义，则 $x$ 的取值范围是
若 $\frac{a}{b}=\frac{2}{3}$ ，则 $\frac{2 a-b}{b}=$
已知 $\triangle A B C$ 中，$A B=2, \angle C=40^{\circ}$ ，现有以下这些条件：（1）$\angle A=30^{\circ}$ ；（2）$\angle A=90^{\circ}$ ；（3） $\angle B=120^{\circ}$ ；（4）$\angle B=140^{\circ}$ ．要使 $\triangle A B C$ 的形状和大小都是确定的，可以添加的条件是 $\_\_\_\_$ ．（写出所有正确结论的序号）
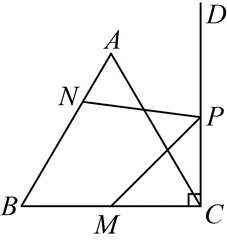
如图，点 $M$ 在等边 $\triangle A B C$ 的边 $B C$ 上，$B M=8$ ，射线 $C D \perp B C$ 垂足为点 $C$ ，点 $P$ 是射线 $C D$ 上一动点，点 $N$ 是线段 $A B$ 上一动点，当 $M P+N P$ 的值最小时，$B N=7$ ，则 $A C$ 的长为
解答题 （共 9 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算：$\sqrt{24} \div \sqrt{3}+\sqrt{6} \times \sqrt{3}-\frac{1}{\sqrt{2}}$ ．
如图，在 $\triangle A B C$ 中，$A D$ 是 $B C$ 边上的中线，分别过点 $B, C$ 作射线 $A D$ 的垂线，垂足为 $E, F$ ，求证：$D E= D F$ ．
先化简，再求值；$\left(\frac{1}{a-2}-\frac{3}{a^2-4}\right) \div \frac{a-1}{a^2+2 a}$ ，其中 $a=\sqrt{2}+2$ ．
某校为了满足同学们体育锻炼的需要，准备购买跳绳和足球若干．已知足球的单价比跳绳的单价多 35元，用 400 元购得的跳绳数量和用 1100 元购得的足球数量相等．求跳绳和足球的单价各是多少元．
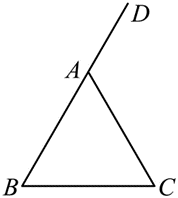
如图，在 $\triangle A B C$ 中，$\angle C A D$ 为 $\triangle A B C$ 的外角．
（1）尺规作图：作 $\angle C A D$ 的平分线 $A E$（保留作图痕迹可加黑，不写作法）；
（2）若 $A B=A C$ ，在（1）的条件下，求证：$A E / / B C$ ．
阅读材料：课本第53页数学活动中介绍一种新的几何图形——“筝形”．定义：两组邻边分别相等的四边形叫做“筝形”．
我们研究一种新几何图形的一般过程：先学习定义，再研究性质和判定．而性质的研究，其实就是对图形边，角，对角线等基本要素的研究．八年级某班按照这样的思路对“筝形”的性质开展研究：
第一步：根据定义剪出一个“筝形”；
第二步：用测量、折纸等方法猜想“筝形”边，角，对角形的结论；
第三步：通过证明得到性质．
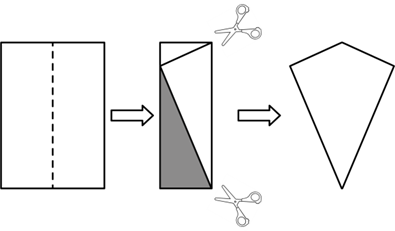
解答问题：
（1）猜想“筝形”的对角线有怎样的结论？请写出来．
（2）请画出图形，写出已知，求证并证明得到对角线的性质．
（3）从性质进一步探究可得到“筝形”的面积公式，请直接写出“筝形”的面积公式．
已知三条线段 $a=4 m n, b=2 m^2+2 n^2, c=(m-n)^2(m n>0$ ，且 $m \neq n)$ ．
（1）证明：线段 $b$ 是这三条线段中最长的线段；
（2）请说明是否能以这三条线段长为边构造三角形．
阅读理解：
材料 1：为了研究分式 $\frac{1}{x}$ 与其分母 $x$ 的数量变化关系，小力制作了表格，并得到如下数据：
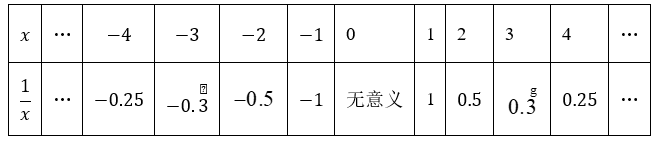
从表格数据观察，当 $x>0$ 时，随着 $x$ 的增大，$\frac{1}{x}$ 的值随之减小，若 $x$ 无限增大，则 $\frac{1}{x}$ 无限接近于 0 ；当 $x < 0$时，随着 $x$ 的增大，$\frac{1}{x}$ 的值也随之减小．
材料 2：在分子、分母都是整式的情况下，如果分子的次数小于分母的次数，称这样的分式为真分式．如果分子的次数大于或等于分母的次数，称这样的分式为假分式。任何一个假分式都可以化为一个整式与一个真分式的和．例如：$\frac{2 x+1}{x-2}=\frac{2 x-4+4+1}{x-2}=\frac{2(x-2)+5}{x-2}=\frac{2(x-2)}{x-2}+\frac{5}{x-2}=2+\frac{5}{x-2}$ ；
根据上述材料完成下列问题：
（1）当 $x>0$ 时，随着 $x$ 的增大， $2+\frac{1}{x}$ 的值 $\_\_\_\_$ （增大或减小）；当 $x < 0$ 时，随着 $x$ 的增大，$\frac{3 x+1}{x}$ 的值．
（增大或减小）；
（2）当 $x>-3$ 时，随着 $x$ 的增大，$\frac{2 x+8}{x+3}$ 的值无限接近一个数，请求出这个数；
（3）如果分式 $\frac{2 x^2-1}{x-1}$ 的值为整数，求 $x$ 的整数值；
（4）当 $0 < x < 1$ 时，直接写出代数式 $\frac{3 x-4}{x-2}$ 值的取值范围是 $\_\_\_\_$ ．
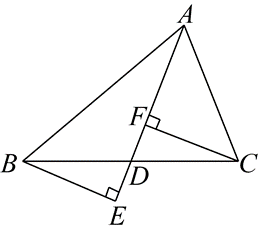
如图，在 $\mathrm{Rt} \triangle A B C$ 中，过点 $B$ 作 $\angle B A C$ 的平分线的垂线，垂足为 $D, B D=A C$
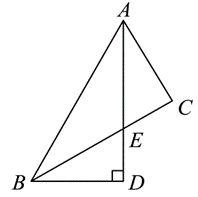
（1）求证：$\angle E B A=\angle E A C$ ；
（2）在射线 $A C$ 上取一点 $F$ ，以 $B F$ 为边，在 $B F$ 的上方作等边三角形 $B F G$ ，过点 $A$ 作直线 $l \| B D$ ．
① 试说明点 $G$ 与直线 $l$ 的位置关系；
② 若 $B D=2$ ，求 $2 C G+A F$ 的最小值．