一、单选题 （共 5 题，每小题 5 分，共 50 分，每题只有一个选项正确）
假设总体 $X$ 服从正态分布 $N\left(\mu, \sigma^2\right), X_1, \cdots, X_n$ 是来自总体 $X$ 的简单随机样本, 其样本均值为 $\bar{X}$, 如果 $P\{|X-\mu| < a\}=P\{|\bar{X}-\mu| < b\}$, 其中 $\sigma>0$, 则有
$\text{A.}$ $a=n b$.
$\text{B.}$ $b=n a$.
$\text{C.}$ $a=\sqrt{n} b$.
$\text{D.}$ $b=\sqrt{n} a$.
设平面区域 $D=\left\{(x, y) \mid 0 \leqslant x \leqslant 2,0 \leqslant y \leqslant 4-x^2\right\}$, 在 $D$ 上随机取一点 $(X, Y)$, 令随机变量 $U=\left\{\begin{array}{ll}0, & X \leqslant 1, \\ 1, & X>1,\end{array} \quad V=\left\{\begin{array}{cc}-1, & Y \leqslant 3, \\ 1, & Y>3,\end{array}\right.\right.$ 则 $U$ 和 $V$ 的相关系数 $\rho_{U V}=(\quad)$.
$\text{A.}$ $\sqrt{\frac{5}{77}}$
$\text{B.}$ $-\sqrt{\frac{5}{77}}$
$\text{C.}$ $\frac{5}{\sqrt{77}}$
$\text{D.}$ $-\frac{5}{\sqrt{77}}$
设二维随机变量 $(X, Y)$ 的分布律
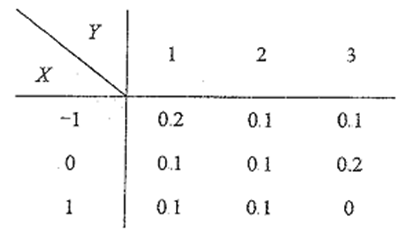
则 $P\{X+Y \leq 1\}=$
$\text{A.}$ 0.4
$\text{B.}$ 0.3
$\text{C.}$ 0.2
$\text{D.}$ 0.1
设随机变量 $X_1, X_2, \cdots, X_{100}$ 独立同分布, $E\left(X_i\right)=0, D\left(X_1\right)=1, i=1,2, \cdots, 100$,则由中心极限定理得 $P\left\{\sum_{i=1}^{100} X_i \leq 10\right\}$ 近似于
$\text{A.}$ 0
$\text{B.}$ $\Phi(1)$
$\text{C.}$ $\Phi(10)$
$\text{D.}$ $\Phi(100)$
设总体 $X \sim N(\mu, 1), Y \sim N(\mu, 1)$, 且 $X, Y$ 相互独立, $X_1, X_2, \cdots, X_n$ 与 $Y_1, Y_2, \cdots, Y_n$ 分别来自总体 $X, Y$ 的简单随机样本, 设 $X=\frac{1}{n} \sum_{i=1}^n X_i, Y=\frac{1}{n} \sum_{i=1}^n Y_i, S_X^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2$, $S_Y^2=\frac{1}{n-1} \sum_{i=1}^n\left(Y_i-\bar{Y}\right)^2$, 则 $\frac{\sqrt{n}(\bar{X}-\bar{Y})}{\sqrt{S_X^2+S_Y^2}}$ 服从
$\text{A.}$ $t(n-1)$
$\text{B.}$ $t(n)$
$\text{C.}$ $t(2 n)$
$\text{D.}$ $t(2 n-2)$
二、填空题 （共 4 题, 每小题 5 分，共 20 分， 请把答案直接填写在答题纸上）
设二维随机变量 $(X, Y)$ 服从正态分布 $N(-1,2 ; 2,2 ; \rho)$, 若 $X+Y$ 与 $X-2 Y$ 相互独立, 则 $\rho=$
已知二维随机变量 $(X, Y)$ 的联合分布律: 要使 $X 、 Y$ 相互独立, 则 $\alpha, \beta$ 的值为
加油站有两套用来加油的设备, 设备 $A$ 是工作人员操作的, 设备 $B$ 是顾客自己操作的, $A 、 B$ 均装有两根加油软管, 任取一时间, $A 、 B$ 正在使用的软管数分别为 $X 、 Y, X 、 Y$ 的联合分布律为下表，求:
(1) $P(X \leq 1, Y \leq 1)$
(2) 至少有一根软管在使用的概率
(3) $P(X=Y)$
(4) $P\{X+Y=2\}$
设 $A 、 B$ 为两个随机事件, $P\{A\}=0.25, P\{B \mid A\}=0.5, P\{A \mid B\}=0.25$, 令随机变量
$$
X=\left\{\begin{array}{rrr}
1 & A \text { 发生 } \\
0 & A \text { 不发生 }
\end{array} \quad Y=\left\{\begin{array}{rr}
1 & B \text { 发生 } \\
0 & B \text { 不发生 }
\end{array}\right.\right.
$$
(1) 求 $(X, Y)$ 的联合分布律
(2) 求 $P\left\{X^2+Y^2=1\right\}$
三、解答题 （ 共 5 题，满分 80 分，解答过程应写出必要的文字说明、证明过程或演算步骤 ）
设随机变量 $X, Y$ 和 $Z$ 相互独立, 且均服从参数为 1 的指数分布. 记
$$
U=\frac{X}{X+Y}, \quad V=\frac{X+Y}{X+Y+Z}, \quad W=X+Y+Z .
$$
(1) 计算随机向量 $(U, V, W)$ 的联合密度函数.
(2) 随机变量 $U, V$ 和 $W$ 是否相互独立? 请证明你的结论.
设随机变量 $X$ 服从参数为 2 的指数分布。
证明: $\bar{Y}=1-e^{-2 X}$ 在区间 $(0,1)$ 上, 服从均匀分布。
设区域 $D=\{(x, y) \mid 0 \leqslant x \leqslant \sqrt{y}, 0 \leqslant y \leqslant 1\}$, 二维随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)= \begin{cases}6 x y, & (x, y) \in D, \\ 0, & \text { 其他. }\end{cases}
$$
(I) 判断 $X, Y$ 是否相互独立;
(II) 求 $Z=\sqrt{X^2+Y}$ 的分布函数.
设总体 $(X, Y)$ 的分布函数为
$$
F(x, y)= \begin{cases}0, & x < 0 \text { 或 } y < \theta, \\ p\left[1-\mathrm{e}^{-(y-\theta)}\right], & 0 \leqslant x < 1, y \geqslant \theta, \\ 1-\mathrm{e}^{-(y-\theta)}, & x \geqslant 1, y \geqslant \theta .\end{cases}
$$
其中 $p, \theta$ 为末知参数, 且 $0 < p < 1$.
(I) 求 $X$ 的概率分布和 $Y$ 的概率密度, 并判别 $X$ 和 $Y$ 的独立性;
(II) 求 $Z=X+Y$ 的概率密度 $f_Z(z)$.
已知编号为 1 的盒子中装有 2 个白球和 1 个红球, 编号为 2 的盒子中装有 3 个白球, 现随机各取一球, 交换放人另一个盒子中, 交换两次, 记 $X$ 为红球所在盒子的编号, $Y$ 服从参数为 1 的指数分布, 随机变量 $X$ 与 $Y$ 相互独立, 令 $Z=\frac{Y}{X}$.
(I) 求 $Z$ 的概率密度;
( II) $Y$ 与 $Z$ 是否相互独立?