单选题 (共 10 题 ),每题只有一个选项正确
如图, I 是全集, M、P、S 是 $I$ 的 3 个子集, 则阴影部分所表示的集合是
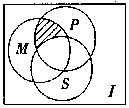
$\text{A.}$ $({M} \cap {P}) \cap {S}$
$\text{B.}$ $({M} \cap {P}) \cup {S}$
$\text{C.}$ $({M} \cap {P}) \cap \bar{S}$
$\text{D.}$ $({M} \cap {P}) \cup \bar{{S}}$
已知映射 ${f}: {AB}$, 其中, 集合 $\mathrm{A}=\{-3,-2,-1,1,2,3,4$,$\} , 集合 \mathrm{B}$ 中的元素都是 A 中元素在映射 $f$ 下的象,且对任意的 $a \in A$ ,在 $B$ 中和它对应的元素是 $\{a\}$ ,则集合 B 中元素的个数是
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 7
若函数 $y=f(x)$ 的反函数是 $y=g(x), f(a)=b, a b \neq 0$ ,则 $g(b)$ 等于
$\text{A.}$ $a$
$\text{B.}$ $a-1$
$\text{C.}$ $b$
$\text{D.}$ $b-1$
函数 ${f}({x})={M} \sin (\omega {x}+\varrho) \quad(\omega>0)$ 在区间 $[{a}, {b}]$ 上是增函数,且 ${f}({a})=-{M}, {f}({b})$ $={M}$ ,则函数 ${g}({x})={M} \cos (\omega {x}+\varrho)$ 在 $[{a}, {b}]$ 上
$\text{A.}$ 是增函数
$\text{B.}$ 是減函数
$\text{C.}$ 可以取得最大值 $M$
$\text{D.}$ 可以取得最小值$-M$
若 $f(x) \sin x$ 是周期为的奇函数,则 $f(x)$ 可以是
$\text{A.}$ $\sin x$
$\text{B.}$ $\cos x$
$\text{C.}$ $\sin 2 x$
$\text{D.}$ $\cos 2 x$
若于毫升水倒人底面半径为 2 cm 的圆杜形器皿中, 量得水面的高度为 6 cm , 若将这些水倒人轴截面是正三角形的倒圆锥形器且中,则水面的高度是
$\text{A.}$ $6 \sqrt{3} \mathrm{~cm}$
$\text{B.}$ $6 \mathrm{~cm}$
$\text{C.}$ $2 \sqrt[3]{18} \mathrm{~cm}$
$\text{D.}$ $3 \sqrt[3]{12} \mathrm{~cm}$
若 $(2 x+\sqrt{3})^4=a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4$, 则 $\left(a_0+a_2+a_4\right)^2-\left(a_1+a_3\right)^2$ 的值为
$\text{A.}$ 1
$\text{B.}$ -1
$\text{C.}$ 0
$\text{D.}$ 2
直线 $\sqrt{3} x+y^2=0$ 截圆 $x^2+y^2=4$ 得的劣弧所对的圆心角为
$\text{A.}$ $\pi / 6$
$\text{B.}$ $\pi / 4$
$\text{C.}$ $\pi / 3$
$\text{D.}$ $\pi / 2$
如图, 在多面体 ABCDEF 中, 已知面 ABCD 是边长为 3 的正方形, $\mathrm{EF} / / \mathrm{AB}$, $\mathrm{EF}=3 / 2, \mathrm{EF}$ 与面 AC 的距离为 2 , 则该多面体的体积为
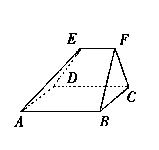
$\text{A.}$ $9 / 2$
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ $15 / 2$
若 $\sin a>\operatorname{tg} a>\operatorname{ctg} a(-\pi / 2 < a < \pi / 2)$, 则 $a \in$
$\text{A.}$ $(-\pi / 2,-\pi / 4)$
$\text{B.}$ $(-\pi / 4,0)$
$\text{C.}$ $(0, \pi / 4)$
$\text{D.}$ $(\pi / 4, \pi / 2)$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
设椭圆 $x^2 / a^2+y^2 / b^2=1(a>b>0)$ 的右焦点为 $F_1$, 右准线为 $l_1$ 。若过 $F_1$ 且垂直于 $x$ 轴的弦的长等于点 $\mathrm{F}_1$ 到 $1_1$ 的距离, 则椭圆的离心率是
若正数 $a 、 b$ 满足 $a b=a+b+3$, 则 $a b$ 的取值范围是
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设复数 $z=3 \cos \theta+\mathrm{i} \cdot 2 \sin \theta, \mathrm{y}=\theta-\arg Z(0 < \theta < \pi / 2)$ 求函数的最大值以及对应的 $\theta$ 值
已知函数 $y=f(x)$ 的图象是自原点出发的一条折线。当 $n \leqslant y \leqslant n+1(n=0,1,2 \ldots$ )时,该图象是斜率为 ${b}^{{n}}$ 的线段(其中正常数 ${b} \neq 1$ ),设数列 $\left\{{x}_{{n}}\right\}$ 由 ${f}\left({x}_{{n}}\right)={n}({n}=1,2, \ldots)$ 定义
(1) 求 ${x}^1 、 {x}^2$ 和 ${x}^n$ 的表达式;
(2) 求 $f(x)$ 的表达式,并写出其定义域:
(3) 证明: $y=f(x)$ 的图象与 $y=x$ 的图象没有横坐标大于 1 的交点。
如图,给出定点 $A (a,0) (a>0)$ 和直线 $l : x=-1, B$ 是直线 $l$ 上的动点, $\angle B O A$ 的角平分线交 $A B$ 于点 $C$ 求点 $C$ 的轨迹方程, 并讨论方程表示的曲线类型与 $a$ 值的关系。
