2023年高考数学第三次模拟考试卷（云南，安徽，黑龙江，山西，吉林五省通用A卷）

导出试卷

2023年高考数学第三次模拟考试卷（云南，安徽，黑龙江，山西，吉林五省通用A卷）

一、单选题（共 8 题），每题只有一个选项正确

1. 已知集合

A = {x ∣ x^{2} \leq 4 x, x \in N_{+}}

, 集合

B = {x ∣ \log_{2} (2^{x} - 4) \leq 2}

, 则

A \cap B =

A.

B.

2,3

C.

{0, 1, 2, 3}

D.

{3}

查看分享下载此题点赞(1) 收藏(0) 错题本(0) 白板加入试卷

2. 设复数

z = 2 + i

的共轭复数为

\bar{z}

, 则

z - \bar{z} + z \bar{z} =

A.

3 + 2 i

B.

3 - 2 i

C.

5 - 2 i

D.

5 + 2 i

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 圆台的上、下底面半径分别是

r = 1, R = 4

, 圆台的高为 4 , 则该圆台的侧面积是

A.

16 π

B.

20 π

C.

25 π

D.

30 π

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 已知

\cos 2 x = - \frac{1}{3}

, 则

\cos^{2} (x - \frac{π}{6}) + \cos^{2} (x + \frac{π}{6})

的值为

A.

\frac{9}{16}

B.

\frac{5}{6}

C.

\frac{13}{20}

D.

\frac{17}{24}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 新能源汽车具有零排放、噪声小、能源利用率高等特点, 近年来备受青睐. 某新能源汽车制造企业为调查其旗下

A

型号新能源汽车的耗电量 (单位:

kW \cdot h / 100 km

) 情况, 随机调查得到了 1200 个样本, 据统计该型号新能源汽车的耗电量

ξ \sim N (13, σ^{2})

, 若

P (12 < ξ < 14) = 0.7

, 则样本中耗电量不小于

^{14} {kW}^{}

h / 100_{km}

的汽车大约有

A.

180 辆

B.

360 辆

C.

600 辆

D.

840 辆

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 已知

O

是坐标原点,

F

是双曲线

E : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)

的左焦点, 平面内一点

M

满足

△ O M F

是等边三角形, 线段

M F

与双曲线

E

交于点

N

, 且

| M N | = | N F |

, 则双曲线

E

的离心率为

A.

\frac{\sqrt{13} + 1}{3}

B.

\frac{\sqrt{13} - 1}{2}

C.

\frac{2 \sqrt{15} + 2}{7}

D.

\frac{2 \sqrt{15} + 1}{7}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 已知直线

l_{1} : x + m y - 3 m - 1 = 0

与

l_{2} : m x - y - 3 m + 1 = 0

相交于点

M

, 线段

A B

是圆

C : (x + 1)^{2} +

(y + 1)^{2} = 4

的一条动弦, 且

| A B | = 2 \sqrt{3}

, 则

\vec{M A} \cdot \vec{M B}

的最小值为

A.

6 - 4 \sqrt{2}

B.

3 - \sqrt{2}

C.

5 + \sqrt{3}

D.

\sqrt{5} - 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 已知函数

f (x)

及其导函数

f^{'} (x)

的定义域均为

R

, 记

g (x) = f^{'} (x)

. 若

f (x + 3)

为奇函数,

g (\frac{3}{2} + 2 x)

为偶函数, 且

g (0) = - 3, g (1) = 2

, 则

\sum_{i = 1}^{2023} g (i) =

A.

670

B.

672

C.

674

D.

676

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、多选题（共 4 题），每题有多个选项正确

9. 若

m > n > 0 > p, m + p \neq 0

, 则

A.

\frac{p}{m} > \frac{p}{n}

B.

m^{2} - p^{2} > 0

C.

\frac{1}{m + n} > \frac{1}{m + p}

D.

m^{2} - n > n^{2} - m

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 某研究机构为了探究吸烟与肺气肿是否有关，调查了200人.统计过程中发现随机从这200人中抽取一人，此人为肺气肿患者的概率为0.1.在制定2×2列联表时，由于某些因素缺失了部分数据，而获得如图所示的2×2列联表，下列结论正确的是

A.

不吸烟患肺气肿的人数为 5 人

B.

200 人中患肺气肿的人数为 10 人

C.

χ^{2}

的观测值

k = 11.42

D.

按

99.9 %

的可靠性要求, 可以认为“吸烟与肺气肿有关系”

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 已知函数

f (x) = \sin (\cos x) + \cos (\sin x)

, 下列关于该函数的结论正确的是

A.

f (x)

的图象关于直线

x = π

对称

B.

f (x)

的一个周期是

2 π

C.

f (x)

在区间

(\frac{π}{2}, π)

上单调递增

D.

f (x)

的最大值为

\sin 1 + 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 定义: 对于定义在区间

I

上的函数

f (x)

和正数

α (0 < α \leq 1)

, 若存在正数

M

, 使得不等式

| f (x_{1}) - f (x_{2}) | \leq

M {| x_{1} - x_{2} |}^{α}

对任意

x_{1}, x_{2} \in I

恒成立, 则称函数

f (x)

在区间

I

上满足

α

阶李普希兹条件, 则下列说法正确的有

A.

函数

f (x) = \sqrt{x}

在

1, + \infty)

上满足

\frac{1}{2}

阶李普希兹条件.

B.

若函数

f (x) = x \ln x

在

[1, e]

上满足一阶李普希兹条件, 则

M

的最小值为 2 .

C.

若函数

f (x)

在

[a, b]

上满足

M = k (0 < k < 1)

的一阶李普希兹条件, 且方程

f (x) = x

在区间

[a, b]

上有解

x_{0}

, 则

x_{0}

是方程

f (x) = x

在区间

[a, b]

上的唯一解.

D.

若函数

f (x)

在

[0, 1]

上满足

M = 1

的一阶李普希兹条件, 且

f (0) = f (1)

, 则存在满足条件的函数

f (x)

, 存在

x_{1}, x_{2} \in [0, 1]

, 使得

| f (x_{1}) - f (x_{2}) | = \frac{2}{3}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、填空题（共 10 题），请把答案直接填写在答题纸上

13. 函数

f (x)

为定义在

R

上的奇函数, 当

x \geq 0

时,

f (x) = 4 x + m

, 则

f (- \frac{1}{2}) =

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14.

(3 x - y + 2 z)^{5}

的展开式中所有不含字母

z

的项的系数之和为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 已知椭圆

C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)

的左、右焦点分别为

F_{1} 、 F_{2}

, 点

A 、 B

在椭圆

C

上, 满足

\vec{A F_{2}} \cdot \vec{F_{1} F_{2}} =

0, \vec{A F_{1}} = λ \vec{F_{1} B}

, 若椭圆

C

的离心率

e \in [\frac{\sqrt{3}}{3}, \frac{\sqrt{2}}{2}]

, 则实数

λ

取值范围为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 古希腊毕达哥拉斯学派的“三角形数”是一列点（或圆球）在等距的排列下可以形成正三角形的数，如1，3，6，10，15，…，我国宋元时期数学家朱世杰在《四元玉鉴》中所记载的“垛积术”，其中的“落一形”锥垛就是每层为“三角形数”的三角锥的锥垛（如图所示，顶上一层1个球，下一层3个球，再下一层6个球…），若一“落一形”三角锥垛有10层，则该锥垛球的总个数为

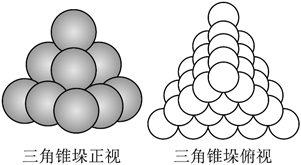
(参考公式:

1^{2} + 2^{2} + 3^{2} + \dots + n^{2} = \frac{n (n + 1) (2 n + 1)}{6} (n \in N^{*})

)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

17. 已知数列

{a_{n}}

满足

a_{n} \neq 0, (1 + 3 a_{1}) (1 + 3 a_{2}) (1 + 3 a_{3}) \dots (1 + 3 a_{n}) = a_{n} (n \in N^{*})

.
(1)证明: 数列

{\frac{1}{a_{n}}}

是等差数列;
(2)求数列

{a_{n} a_{n + 1}}

的前

n

项和

T_{n}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 在(1)

2 a \cos C = 2 b - c

, (2)

\sqrt{3} b \cos \frac{B + C}{2} = a \sin B

, (3)

a \sin C = c \cos (A - \frac{π}{6})

这三个条件中任选一个作为条件, 补充到下面问题中, 然后解答.
已知锐角

△ A B C

的内角

A, B, C

所对的边分别为

a, b, c

, 且 (填序号).
(1)若

a = \sqrt{3}, \cos (B - C) = \frac{9}{10}

, 求

△ A B C

的面积;
(2)求

\frac{b + c}{a}

的取值范围.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

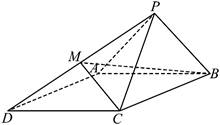
19. 如图, 已知四棱雉

P - A B C D

的底面为菱形, 且

∠ A B C = 60^{\circ}, A B = P C = 2, P A = P B = \sqrt{2} \cdot M

是棱

P D

上的点, 且四面体

M P B C

的体积为

\frac{\sqrt{3}}{6}

.
(1)证明:

P M = M D

;
(2) 若过点

C, M

的平面

α

与

B D

平行, 且交

P A

于点

Q

, 求平面

B C Q

与平面

A B C D

夹角的余弦值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 为普及航空航天科技相关知识､发展青少年航空航天科学素养，贵州省某中学组织开展“筑梦空天”航空航天知识竞赛.竞赛试题有甲、乙、丙三类（每类题有若干道），各类试题的每题分值及小明答对概率如下表所示，各小题回答正确得到相应分值，否则得0分，竞赛分三轮答题依次进行，各轮得分之和即为选手总分.

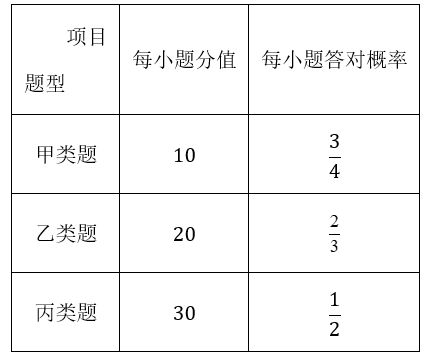
其竞赛规则为：
第一轮，先回答一道甲类题，若正确，进入第二轮答题；若错误，继续回答另一道甲类题，该题回答正确，同样进入第二轮答题，否则，退出比赛.
第二轮，在乙类题或丙类题中选择一道作答，若正确，进入第三轮答题；否则，退出比赛.
第三轮，在前两轮未作答的那一类试题中选择一道作答.
小明参加竞赛，有两种方案选择，方案一：先答甲类题，再答乙类题，最后答丙类题；
方案二：先答甲类题，再答丙类题，最后答乙类题.各题答对与否互不影响.请完成以下解答：
(1)若小明选择方案一，求答题次数恰好为3次的概率；
(2)经计算小明选择方案一所得总分的数学期望为125/4，为使所得总分的数学期望最大，小明该选择哪一种方案？并说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 抛物线

C : y^{2} = 2 p x (p > 0)

上的点

M (1, y_{0})

到抛物线

C

的焦点

F

的距离为

2, A 、 B

(不与

O

重合) 是抛物线

C

上两个动点, 且

O A ⊥ O B

.
(1)求抛物线

C

的标准方程;
(2)

x

轴上是否存在点

P

使得

∠ A P B = 2 ∠ A P O

? 若存在, 求出点

P

的坐标, 若不存在, 说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

22. 已知函数

f (x) = \ln x + \frac{a}{x}

的图象在

x = 1

处的切线方程为

y = b

.
(1)求

a, b

的值及

f (x)

的单调区间.
(2) 已知

F (x) = \frac{x e^{x} f (x) - e^{x} + m x}{x^{2} - x}

, 是否存在实数

m

, 使得曲线

y = F (x)

恒在直线

y = x + 1

的上方? 若存在, 求出实数

m

的值; 若不存在, 请说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。