单选题 (共 1 题 ),每题只有一个选项正确
如图所示,空间存在竖直向上的匀强磁场,磁感应强度大小为B,足够长的光滑平行金属导轨水平放置,导轨左右两部分的间距分别为l、2l;质量分别为m、2m 的导体棒a、b均垂直导轨放置,导体棒a接入电路的电阻为R,其余电阻均忽略不计;a、b两棒分别以v0、2v0的初速度同时向右运动,两棒在运动过程中始终与导轨垂直且保持良好接触,a 总在窄轨上运动,b总在宽轨上运动,直到两棒达到稳定状态,从开始运动到两棒稳定的过程中,
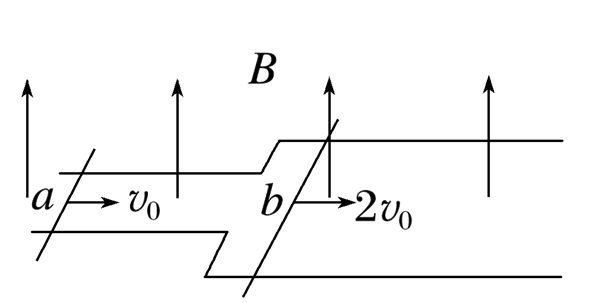
下列说法正确的是
$\text{A.}$ $a$ 棒加速度的大小始终等于 $b$ 棒加速度的大小
$\text{B.}$ 稳定时 $a$ 棒的速度为 $1.5 v_0$
$\text{C.}$ 电路中产生的焦耳热为 $\frac{3}{2} m v_0^2$
$\text{D.}$ 通过导体棒 $a$ 的某一横截面的电荷量为 $\frac{m v_0}{2 B l}$
多选题 (共 6 题 ),每题有多个选项正确
如图所示,一质量为2m的足够长U形光滑金属框abcd置于水平绝缘平台上,bc边长为L,不计金属框电阻.一长为L的导体棒MN置于金属框上,导体棒的阻值为R、质量为m.装置处于磁感应强度为B、方向竖直向下的匀强磁场中.现给金属框水平向右的初速度v0,在整个运动过程中MN始终与金属框保持良好接触,则 A.刚开始运动时产生的感应电流方向为M→N→c→b→M
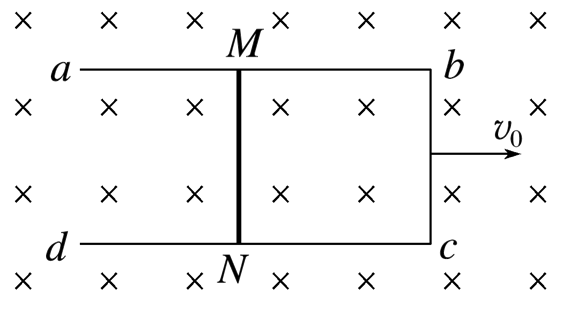
$\text{A.}$ 刚开始运动时产生的感应电流方向为 $M \rightarrow N \rightarrow c \rightarrow b \rightarrow M$
$\text{B.}$ 导体棒的最大速度为 $\frac{v_0}{2}$
$\text{C.}$ 通过导体棒的电荷量为 $\frac{2 m v_0}{3 B L}$
$\text{D.}$ 导体棒产生的焦耳热为 $\frac{5}{6} m v_0{ }^2$
如图所示,半径为r的粗糙四分之一圆弧导轨与光滑水平导轨平滑相连,四分之一圆弧导轨区域没有磁场,水平导轨区域存在磁感应强度大小为B、方向竖直向上的匀强磁场,导轨间距为l,ab、cd是质量为m、接入电路中电阻为R的金属棒,导轨电阻忽略不计.cd静止在平滑轨道上,ab从四分之一圆弧轨道顶端由静止释放,在圆弧轨道上克服阻力做功 mgr,水平导轨足够长,ab、cd始终与导轨垂直并接触良好,且不会相撞,重力加速度为g.从ab棒进入水平轨道开始,
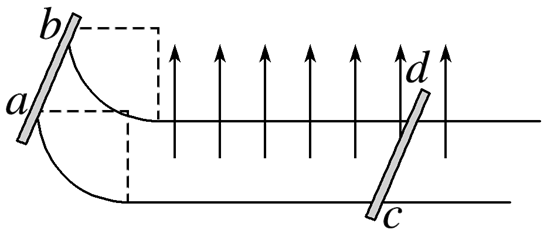
下列说法正确的是
下列说法正确的是
$\text{A.}$ $a b$ 棒先做匀减速运动,最后做匀速运动
$\text{B.}$ $c d$ 棒先做匀加速直线运动,最后和 $a b$ 以相同的速度做匀速运动
$\text{C.}$ $ a b$ 棒刚进入磁场时,$c d$ 棒电流为 $\frac{B l \sqrt{g r}}{2 R}$
$\text{D.}$ $a b$ 棒的最终速度大小为 $\frac{\sqrt{g r}}{2}$
如图,相距为L的两光滑平行金属导轨固定在绝缘水平桌面上,左端接一电容器C,阻值为R的电阻通过三角旋钮开关S与两导轨连接,长度为L、质量为m的金属杆ab垂直导轨放置,且与导轨始终接触良好,两导轨间存在垂直导轨平面向下的匀强磁场,磁感应强度大小为B.三角旋钮开关S仅1、2之间导电,S左旋时能将电阻R和电容器C接入同一回路,右旋时能将电阻R和金属杆ab接入同一回路,初始时1、2连接电容器和金属杆,现用恒力F向右拉金属杆ab,使其从静止开始运动,经一段时间后撤去F,同时旋转S,此时金属杆的速度大小为v0,不计金属杆和导轨的电阻.

下列说法正确的是
$\text{A.}$ 撤去 $F$ 前,金属杆做变加速直线运动
$\text{B.}$ 撤去 $F$ 同时向右旋开关 S ,金属杆做加速度减小的减速运动
$\text{C.}$ 恒力 $F$ 对金属杆做的功等于 $\frac{1}{2} m v_0{ }^2$
$\text{D.}$ 若分别左旋右旋 S ,两种情况下,通过电阻 $R$ 的电荷量之比为 $C B^2 L^2: m$
如图,足够长的平行光滑金属导轨 $M 、 N$ 固定在水平桌面上,导轨间距离为 $L$ ,垂直导轨平面有坚直向下的匀强磁场,以 $C D$ 为分界线,左边磁感应强度大小为 $2 B$ ,右边为 $B$ ,两导体棒 $a 、 b$ 垂直导轨静止放置,$a$ 棒距 $C D$ 足够远,已知 $a$ 、 $b$ 棒质量均为 $m$ 、长度均为 $L$ 、电阻均为 $r$ ,棒与导轨始终接触良好,导轨电阻不计,现使 $a$ 获得一瞬时水平速度 $v_0$ ,在两棒运动至稳定的过程中 $(a$棒还没到 $C D$ 分界线),下列说法正确的是
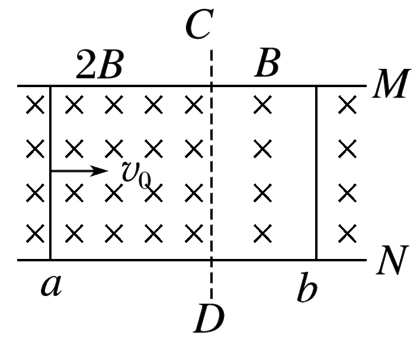
$\text{A.}$ $a 、 b$ 系统机械能守恒
$\text{B.}$ $a 、 b$ 系统动量不守恒
$\text{C.}$ 通过导体棒 $a$ 的电荷量为 $\frac{2 m v_0}{5 B L}$
$\text{D.}$ 导体棒 $a$ 产生的焦耳热为 $\frac{2 m v_0{ }^2}{5}$
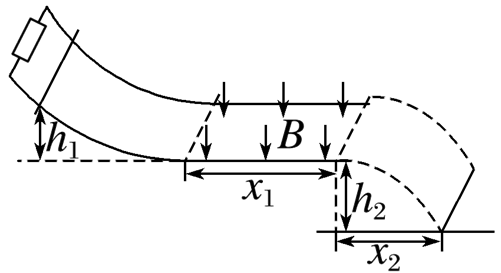
如图所示,一光滑轨道固定在架台上,轨道由倾斜和水平两段组成,倾斜段的上端连接一电阻R=0.5 Ω,两轨道间距d=1 m,水平部分两轨道间有一竖直向下,磁感应强度B=0.5 T的匀强磁场.一质量m=0.5 kg、长为l=1.1 m、电阻忽略不计的导体棒,从轨道上距水平面h1=0.8 m高处由静止释放,通过磁场区域后从水平轨道末端水平飞出,落地点与水平轨道末端的水平距离x2=0.8 m,水平轨道距水平地面的高度h2=0.8 m.通过计算可知(g取10 m/s2)
$\text{A.}$ 导体棒进入磁场时的速度为3 m/s
$\text{B.}$ 导体棒整个运动过程中,电阻R上产生的热量为3 J
$\text{C.}$ 磁场的长度x1为2 m
$\text{D.}$ 整个过程通过电阻的电荷量为2 C
如图所示,平行金属导轨AHQD、PNM上放置有一导体棒 $a b$ ,导轨倾斜部分置于坚直向上、磁感应强度大小为 $B$ 的匀强磁场中,导轨 $A H Q D$ 水平部分通过导线分别连接有电容器(电容为 $C$ )和定值电阻 (阻值为 $R$ ),导轨 $M$ 端接有一单刀双掷开关,导轨间距为 $L$ ,导轨倾斜部分的倾角为 $\theta$ ,导体棒与导轨间的动摩擦因数为 $\mu(\mu < \tan \theta)$ ,导体棒质量为 $m$ ,导轨、导体棒和导线的电阻忽略不计,重力加速度 $g=$ $10 m / s ^2$ .现在离 $H N$ 足够远处由静止释放导体棒 $a b$ ,导体棒可沿导轨向下运动,导体棒始终与导轨垂直且接触良好,则

$\text{A.}$ 断开开关时,导体棒做加速度减小的加速运动,最后匀速下滑
$\text{B.}$ 开关接 1 ,若导体棒运动距离为 $s$ 时,速度为 $v$ ,则所用时间 $t=\frac{m v R+B^2 L^2 s(\cos \theta+\mu \sin \theta) \cos \theta}{m g R(\sin \theta-\mu \cos \theta)}$
$\text{C.}$ 开关接 2 ,导体棒匀加速下滑
$\text{D.}$ 开关接 2 ,通过导体棒的电流 $I=\frac{m g(\sin \theta-\mu \cos \theta) C B L \cos \theta}{m+C B^2 L^2 \cos \theta(\cos \theta+\mu \sin \theta)}$
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图所示,平行光滑金属双导轨 $P_1 Q_1 M_1$ 和 $P_2 Q_2 M_2$ ,其中 $P_1 Q_1$ 和 $P_2 Q_2$ 为半径 $r=0.8 m$ 的 $\frac{1}{4}$ 光滑圆轨道,$O_1$ 和 $O_2$ 为对应圆轨道的圆心,$Q_1 、 Q_2$ 在 $O_1$ 、 $O_2$ 正下方且为圆轨道和水平轨道的平滑连接点,$Q_1 M_1$ 和 $Q_2 M_2$ 为足够长的水平轨道,水平轨道处于坚直向上的匀强磁场中,磁感应强度 $B=1 T$ ,导轨间距 $L=1 m$ ;两导体棒 $a 、 b$ 始终垂直于两导轨且与导轨接触良好, $a 、 b$ 的质量均为 1 kg ,电阻均为 $1 \Omega$ ,导轨电阻不计.初始时刻,$b$ 静止在水平导轨上,$a$ 从与圆心等高的 $P_1 P_2$ 处由
静止释放,$a 、 b$ 在以后运动的过程中不会
发生碰撞 $\left(g=10 m / s ^2\right)$ .求:

(1)导体棒a从Q1Q2进入磁场时,导体棒b的加速度大小;
(2)导体棒a、b稳定时的速度大小;
(3)整个过程中,通过导体棒b的电荷量.