多选题 (共 4 题 ),每题有多个选项正确
已知 $m, n$ 是两条不同的直线,$\alpha, \beta$ 是两个不同的平面,则( )
$\text{A.}$ 若 $m / / n, n \subset \alpha$ ,则 $m / / \alpha$
$\text{B.}$ 若 $m \perp n, n \subset \alpha$ ,则 $m \perp \alpha$
$\text{C.}$ 若 $m \perp \alpha, n \perp \alpha$ ,则 $m / / n$
$\text{D.}$ 若 $m / / \alpha, m / / \beta, \alpha \cap \beta=n$ ,则 $m / / n$
已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $3 a$ ,点 $M$ 是棱 $B C$ 上的定点,且 $B M=2 C M$ .点 $P$ 是棱 $C_1 D_1$ 上的动点,则
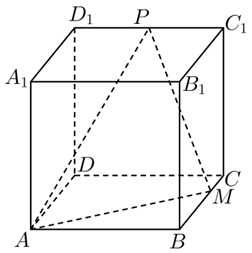
$\text{A.}$ 当 $P C_1=\frac{2}{3} a$ 时,$\triangle P A M$ 是直角三角形
$\text{B.}$ 四棱锥 $A_1-P A M$ 的体积最小值为 $\frac{3}{2} a^3$
$\text{C.}$ 存在点 $P$ ,使得直线 $B D_1 \perp$ 平面 $P A M$
$\text{D.}$ 任意点 $P$ ,都有直线 $B B_1 / /$ 平面 $P A M$
设 $a, b$ 是两条不同的直线,$\alpha, \beta, \gamma$ 是三个不同的平面,$P$ 是一个点,则下列选项正确的为( )
$\text{A.}$ 若 $\alpha / / \beta, a \subset \alpha$ ,则 $a / / \beta$
$\text{B.}$ 若 ${ }^1{ }^1{ }_b^1, a \perp \alpha, b \perp \beta$ ,则 $\alpha \perp \beta$
$\text{C.}$ 若 $\alpha \perp \beta, \alpha I \beta=b, P \in \alpha, P \in a, \stackrel{1}{a} \perp \stackrel{1}{b}$ ,则 $a \perp \beta$
$\text{D.}$ 若 $\alpha \perp \gamma, \alpha / / \beta$ ,则 $\beta \perp \gamma$
在三棱锥 $D-A B C$ 中,已知 $A B=B C=2, A C=2 \sqrt{3}, D B=4$ ,平面 $B C D \perp$ 平面 $A B C$ ,且 $D B \perp A B$ ,则( ).
$\text{A.}$ $D B \perp A C$
$\text{B.}$ 平面 $D A B \perp$ 平面 $A B C$
$\text{C.}$ 三棱锥 $D-A B C$ 的体积为 $\frac{4 \sqrt{3}}{3}$
$\text{D.}$ 三棱锥 $D-A B C$ 的外接球的表面积为 $16 \pi$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图所示,平面 $ABCD \perp$ 平面 BCE ,四边形 ABCD 为矩形, $BC = CE$ ,点 F 为 CE 的中点.
(1)证明: $AE / /$ 平面 BDF ;
(2)点 M 为 CD 上任意一点,在线段 AE 上是否存在点 P ,使得 $PM \perp BE$ ?若存在,确定点 P 的位置,并加以证明;若不存在,请说明理由.
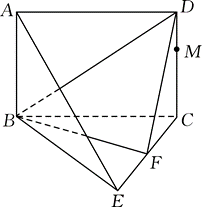
如图,在三棱台 $ABC - DEF$ 中, $CF \perp$ 平面 $DEF , AB \perp BC$ .
(1)设平面 $ACE \cap$ 平面 $DEF = a$ ,求证: $DF / / a$ ;
(2)若 $EF = CF =2 BC$ ,试问在线段 BE 上是否存在点 G ,使得平面 $DFG \perp$ 平面 CDE ?若存在,请确定点 G 的位置;若不存在,请说明理由.