已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $3 a$ ,点 $M$ 是棱 $B C$ 上的定点,且 $B M=2 C M$ .点 $P$ 是棱 $C_1 D_1$ 上的动点,则
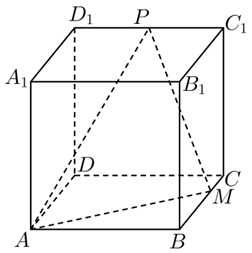
A
当 $P C_1=\frac{2}{3} a$ 时,$\triangle P A M$ 是直角三角形
B
四棱锥 $A_1-P A M$ 的体积最小值为 $\frac{3}{2} a^3$
C
存在点 $P$ ,使得直线 $B D_1 \perp$ 平面 $P A M$
D
任意点 $P$ ,都有直线 $B B_1 / /$ 平面 $P A M$
E
F