单选题 (共 14 题 ),每题只有一个选项正确
函数 $y=f(x)$ 的图象由 $y=\cos \left(2 x+\frac{\pi}{6}\right)$ 的图象向左平移 $\frac{\pi}{6}$ 个单位长度得到,则 $y=f(x)$ 的图象与直线 $y=\frac{1}{2} x-\frac{1}{2}$ 的交点个数为( )
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
已知函数 $f(x)=\sin (\omega x+\varphi)$ 在区间 $\left(\frac{\pi}{6}, \frac{2 \pi}{3}\right)$ 单调递增,直线 $x=\frac{\pi}{6}$ 和 $x=\frac{2 \pi}{3}$ 为函数 $y=f(x)$ 的图象的两条对称轴,则 $f\left(-\frac{5 \pi}{12}\right)=$
$\text{A.}$ $-\frac{\sqrt{3}}{2}$
$\text{B.}$ $-\frac{1}{2}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{\sqrt{3}}{2}$
将函数 $f(x)=\sin \left(\omega x+\frac{\pi}{3}\right)(\omega > 0)$ 的图象向左平移 $\frac{\pi}{2}$ 个单位长度后得到曲线 $C$ ,若 $C$ 关于 $y$ 轴对称,则 $\omega$ 的最小值是( )
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{2}$
设函数 $f(x)=\sin \left(\omega x+\frac{\pi}{3}\right)$ 在区间 $(0, \pi)$ 恰有三个极值点、两个零点,则 $\omega$ 的取值范围是( )
$\text{A.}$ $\left[\frac{5}{3}, \frac{13}{6}\right)$
$\text{B.}$ $\left[\frac{5}{3}, \frac{19}{6}\right)$
$\text{C.}$ $\left(\frac{13}{6}, \frac{8}{3}\right]$
$\text{D.}$ $\left(\frac{13}{6}, \frac{19}{6}\right]$
记函数 $f(x)=\sin \left(\omega x+\frac{\pi}{4}\right)+b(\omega > 0)$ 的最小正周期为 $T$ .若 $\frac{2 \pi}{3} < T < \pi$ ,且 $y=f(x)$ 的图象关于点 $\left(\frac{3 \pi}{2}\right.$ , 2)中心对称,则 $f\left(\frac{\pi}{2}\right)=($
$\text{A.}$ 1
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ 3
把函数 $y=f(x)$ 图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ 倍,纵坐标不变,再把所得曲线向右平移 $\frac{\pi}{3}$ 个单位长度,得到函数 $y=\sin \left(x-\frac{\pi}{4}\right)$ 的图象,则 $f(x)=(\quad)$
$\text{A.}$ $\sin \left(\frac{x}{2}-\frac{7 \pi}{12}\right)$
$\text{B.}$ $\sin \left(\frac{x}{2}+\frac{\pi}{12}\right)$
$\text{C.}$ $\sin \left(2 x-\frac{7 \pi}{12}\right)$
$\text{D.}$ $\sin \left(2 x+\frac{\pi}{12}\right)$
下列区间中,函数 $f(x)=7 \sin \left(x-\frac{\pi}{6}\right)$ 单调递增的区间是
$\text{A.}$ $\left(0, \frac{\pi}{2}\right)$
$\text{B.}$ $\left(\frac{\pi}{2}, \pi\right)$
$\text{C.}$ $\left(\pi, \frac{3 \pi}{2}\right)$
$\text{D.}$ $\left(\frac{3 \pi}{2}, 2 \pi\right)$
为了得到函数 $y=\sin \left(2 x-\frac{\pi}{6}\right)$ 的图象,可以将函数 $y=\sin 2 x$ 的图象(
$\text{A.}$ 向右平移 $\frac{\pi}{6}$ 个单位长度
$\text{B.}$ 向右平移 $\frac{\pi}{12}$ 个单位长度
$\text{C.}$ 向左平移 $\frac{\pi}{6}$ 个单位长度
$\text{D.}$ 向左平移 $\frac{\pi}{12}$ 个单位长度
若函数 $f(x)=\sqrt{3} \sin \omega x-\cos \omega x, \omega > 0, x \in \mathbf{R}$ ,又 $f\left(x_{1}\right)=2, f\left(x_{2}\right)=0$ ,且 $\left|x_{1}-x_{2}\right|$ 的最小值为 $\frac{3}{8} \pi$ ,则 $\omega$ 的值为( )
$\text{A.}$ $\frac{4}{3}$
$\text{B.}$ $\frac{8}{3}$
$\text{C.}$ 4
$\text{D.}$ $\frac{16}{3}$
已知函数 $y=g(x)$ 的图象与函数 $y=\sin 2 x$ 的图象关于直线 $x=\pi$ 对称,将 $g(x)$ 的图象向右平移 $\frac{\pi}{3}$ 个单位长度后得到函数 $y=f(x)$ 的图象,则函数 $y=f(x)$ 在 $x \in\left[0, \frac{\pi}{2}\right]$ 时的值域为( )
$\text{A.}$ $\left[-\frac{\sqrt{3}}{2}, \frac{\sqrt{3}}{2}\right]$
$\text{B.}$ $\left[-1, \frac{\sqrt{3}}{2}\right]$
$\text{C.}$ $\left[-\frac{\sqrt{3}}{2}, 1\right]$
$\text{D.}$ $[0,1]$
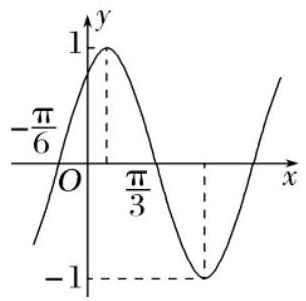
已知函数 $f(x)=\sin (\omega x+\varphi)\left(A>0, \omega>0,|\varphi| < \frac{\pi}{2}\right)$ 的部分图象如图所示,则()
$\text{A.}$ $f(x)=2 \sin \left(2 x+\frac{\pi}{3}\right)$
$\text{B.}$ $f(x)=2 \sin \left(2 x-\frac{\pi}{3}\right)$
$\text{C.}$ $f(x)=2 \sin \left(x+\frac{\pi}{6}\right)$
$\text{D.}$ $f(x)=2 \sin \left(\frac{1}{2} x-\frac{\pi}{6}\right)$
记函数 $f(x)=\cos \left(\omega x+\frac{\pi}{3}\right)+b(\omega > 0)$ 的最小正周期为 $T$ ,若 $\pi < T < \frac{3 \pi}{2}$ ,且 $(\pi, 2)$ 是 $y=f(x)$ 图象的一个最高点,则 $f\left(\frac{\pi}{4}\right)=$
$\text{A.}$ $1-\frac{\sqrt{2}}{2}$
$\text{B.}$ $1+\frac{\sqrt{2}}{2}$
$\text{C.}$ $2-\frac{\sqrt{2}}{2}$
$\text{D.}$ $2+\frac{\sqrt{2}}{2}$
为了得到函数 $y=\sin 2 x$ 的图象,只需把函数 $y=\sin \left(2 x+\frac{\pi}{2}\right)$ 的图象( )
$\text{A.}$ 向左平移 $\frac{\pi}{2}$ 个单位
$\text{B.}$ 向右平移 $\frac{\pi}{2}$ 个单位
$\text{C.}$ 向左平移 $\frac{\pi}{4}$ 个单位
$\text{D.}$ 向右移 $\frac{\pi}{4}$ 个单位
把函数 $y=f(x)$ 图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ 倍,纵坐标不变,再把所得曲线向右平移 $\frac{\pi}{3}$ 个单位长度,得到函数 $y=\sin \left(x-\frac{\pi}{4}\right)$ 的图象,则 $f(x)=(\quad)$
$\text{A.}$ $\sin \left(\frac{x}{2}-\frac{7 \pi}{12}\right)$
$\text{B.}$ $\sin \left(\frac{x}{2}+\frac{\pi}{12}\right)$
c. $\sin \left(2 x-\frac{7 \pi}{12}\right)$
$\text{C.}$ $\sin \left(2 x+\frac{\pi}{12}\right)$
多选题 (共 3 题 ),每题有多个选项正确
要得到 $y=\cos 2 x$ 的图象 $C_{1}$ ,只要将 $y=\sin \left(2 x+\frac{\pi}{3}\right)$ 图象 $C_{2}$ 怎样变化得到
$\text{A.}$ 将 $y=\sin \left(2 x+\frac{\pi}{3}\right)$ 的图象 $C_{2}$ 沿 $x$ 轴方向向左平移 $\frac{\pi}{12}$ 个单位
$\text{B.}$ 将 $y=\sin \left(2 x+\frac{\pi}{3}\right)$ 的图象 $C_{2}$ 沿 $x$ 轴方向向右平移 $\frac{11 \pi}{12}$ 个单位
$\text{C.}$ 先作 $C_{2}$ 关于 $x$ 轴对称图象 $C_{3}$ ,再将图象 $C_{3}$ 沿 $x$ 轴方向向右平移 $\frac{5 \pi}{12}$ 个单位
$\text{D.}$ 先作 $C_{2}$ 关于 $x$ 轴对称图象 $C_{3}$ ,再将图象 $C_{3}$ 沿 $x$ 轴方向向左平移 $\frac{\pi}{12}$ 个单位
将函数 $f(x)=\sin (\omega x+\varphi)$ 的图象向左平移 $\frac{\pi}{6}$ 个单位长度后得到 $y=g(x)$ 的图象如图,则
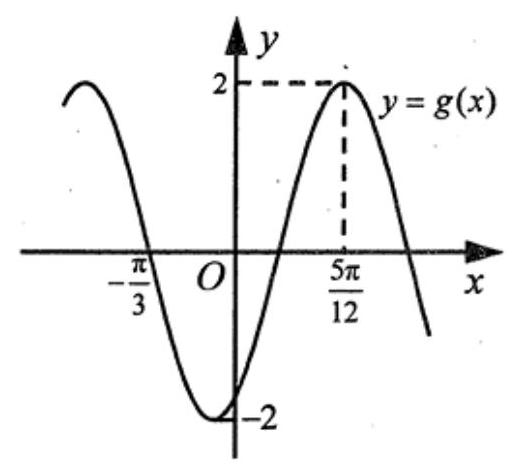
$\text{A.}$ $f(x)$ 为奇函数
$\text{B.}$ $f(x)$ 在区间 $\left(\frac{\pi}{6}, \frac{\pi}{2}\right)$ 上单调递增
$\text{C.}$ 方程 $f(x)=1$ 在 $(0,2 \pi)$ 内有 4 个实数根
$\text{D.}$ $f(x)$ 的解析式可以是 $f(x)=2 \sin \left(2 x-\frac{\pi}{3}\right)$
以下关于函数 $f(x)=\sin 2 x+\sqrt{3} \cos 2 x$ 的命题,正确的是( )
$\text{A.}$ 函数 $y=f(x)$ 的最小正周期为 $\pi$
$\text{B.}$ 点 $\left(\frac{\pi}{12}, 0\right)$ 是函数 $y=f(x)$ 图象的一个对称中心
$\text{C.}$ 直线 $x=\frac{\pi}{3}$ 的函数 $y=f(x)$ 图象的一条对称轴
$\text{D.}$ 将函数 $y=f(x)$ 的图象向右平移 $\frac{\pi}{6}$ 个单位后得到的函数的图象关于原点对称