单选题 (共 10 题 ),每题只有一个选项正确
在四个数 $-2,-0.6, \frac{1}{2}, \sqrt{3}$ 中, 最小的数是
$\text{A.}$ $-2$
$\text{B.}$ $-0.6$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\sqrt{3}$
2022 年 4 月 16 日央视新闻网全程直播 “神般十三号” 载人飞船返航, 截止当天下午五 时, 全网共 $2728.9$ 万人在线观看. 数据 $2728.9$ 万用科学记数法表示为
$\text{A.}$ $2728.9 \times 10^4$
$\text{B.}$ $2.7289 \times 10^4$
$\text{C.}$ $2.7289 \times 10^7$
$\text{D.}$ $2.7289 \times 10^{-7}$
下列图案中, 既是中心对称图形又是轴对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
下列运算结果正确的是
$\text{A.}$ $\left(a^2\right)^3=a^5$
$\text{B.}$ $-a^2 b \div a^2=-b$
$\text{C.}$ $-3 a^2 b-2 a^2 b=-a^2 b$
$\text{D.}$ $(a-b)^2=a^2-b^2$
在平面直角坐标系中, 点 $A(1,3)$. 关于 $x$ 轴对称点的点 $B$ 所在的象限是
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
某车间 20 名工人日加工零件数如表所示:

这些工人日加工零件数的众数、中位数分别是
$\text{A.}$ $5 、 6$
$\text{B.}$ $5 、 5$
$\text{C.}$ $6 、 7$
$\text{D.}$ $6 、 6$
下列命題是假命题的是
$\text{A.}$ 平分弦的直径垂直于这条弦
$\text{B.}$ 三角形两条内角角平分线的交点是三角形的内心
$\text{C.}$ 菱形的对角线互相垂直
$\text{D.}$ 直角三角形中 $30^{\circ}$ 角所对的直角边等于斜边的一半
如图, $A B / / C D, A E$ 平分 $\angle C A B$ 交 $C D$ 于点 $E$. 若 $\angle C=50^{\circ}$, 则 $\angle A E C$ 的大小为
$\text{A.}$ $55^{\circ}$
$\text{B.}$ $65^{\circ}$
$\text{C.}$ $75^{\circ}$
$\text{D.}$ $85^{\circ}$
如图, 圆锥的底面半径为 5 , 高为 12 , 则该圆锥的侧面积为
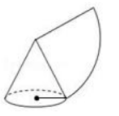
$\text{A.}$ $30 \pi$
$\text{B.}$ $60 \pi$
$\text{C.}$ $65 \pi$
$\text{D.}$ $90 \pi$
如图, 在平面直角坐标系中, $\angle A O B=90^{\circ}, \angle O A B=30^{\circ}$, 反比例函数 $y_1=\frac{m}{x}(m \neq 0)$ 的图象经过点 $A$, 反比例函数 $y_2=\frac{n}{x}(n \neq 0)$ 的图象经过点 $B$, 若 $n=-1$, 则 $m$ 的值是

$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
填空题 (共 6 题 ),请把答案直接填写在答题纸上
使函数表达式 $y=\sqrt{x+1}$ 有意义的自变量 $x$ 的取值范围是
若 $m$ 是方程 $2 x^2-3 x-2=0=0$ 的一个根, 则 $-2 m^2+3 m+19$ 的值为
将 2 本艺术类、 4 本文学类、 6 本科技类的书籍混在一起. 若小陈从中随机抽取一本, 则抽中文学类的概率为
若一个正多边形的每一个内角都是 $150^{\circ}$, 则这个正多边形的边数是
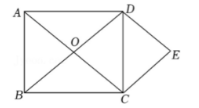
如图, 矩形 $A B C D$ 的对角线 $A C, B D$ 相交于点 $O, D E / / A C, C E / / B D$. 若 $A C=10$, 则 四边形 $O C E D$ 的周长是 .
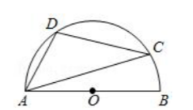
如图, $A B$ 是半圆的直径, $C 、 D$ 是半圆上的两点, $\angle A D C=100^{\circ}$, 则 $\angle C A B$ 等于
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $(-1)^{2022}+|-\sqrt{2}|+\left(\frac{1}{2}\right)^{-1}-\sqrt{8}$.
先化简, 再求值: $\frac{6 a}{a^2-9} \div\left(1+\frac{2 a-3}{a+3}\right)$, 其中 $a=4$.
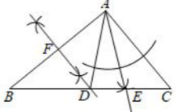
如图, 在 $\triangle A B C$ 中, $\angle B=35^{\circ}, \angle C=50^{\circ}$.
(1) 通过观察尺规作图的痕迹, 可以发现直线 $D F$ 是线段 AB的 ( ) . 射线$AE$是$ \angle DAC$的 ( )
(2) 在 (1) 所作的图中, 求 $\angle D A E$ 的度数.
为落实 “双减提质”, 进一步深化 “数学提升工程”, 提升学生数学核心素养, 某学校拟 开展 “双减” 背景下的初中数学活动型作业成果展示现场会, 为了解学生最喜爱的项目, 现随机抽取若干名学生进行调查, 并将调查结果绘制成如下两幅不完整的统计图:

根据以上信息, 解答下列问题:
(1) 参与此次抽样调查的学生人数是 ( ) 人, 补全统计图(1):
(2) 图(2)中扇形 $D$ 的圆心角度数为 ( ) 度;
(3) 若参加成果展示活动的学生共有 2400 人, 估计其中最喜爱 “测量” 项目的学生人 数是多少;
(4) 计划在 $A, B, C, D, E$ 五项活动中随机选取两项作为直播项目, 请用列表或画树 状图的方法, 求恰好选中 $B, E$ 这两项活动的概率. $\frac{1}{10}$
如图, 在 $\triangle A B C$ 中, $A D \perp B C$ 于点 $D, E, F$ 分别是 $A C, A B$ 的中点, $O$ 是 $D F$ 的中点, $E O$ 的延长线交线段 $B D$ 于点 $G$, 连结 $D E, E F, F G$.
(1) 求证: 四边形 $D E F G$ 是平行四边形.
(2) 当 $A D=5, D C=2$ 时, 求 $F G$ 的长.

我国传统数学名著《九章算术》记载: “今有对兔同笼, 上有三十五头, 下有九十四足, 问鸡兔各几何? "译文: 有若干只鸡与兔在同一个笼子里, 从上面数有 35 个头, 从下面 数有 94 只脚, 问笼中各有几只鸡和兔? 根据以上译文, 回智以下问题:
(1)笼中鸡、兔各有多少只?
(2) 若还是 94 只脚, 但不知道头多少个, 笼中鸡兔至少 30 只且不超过 40 只. 问这笼 鸡兔最多有多少只鸡?
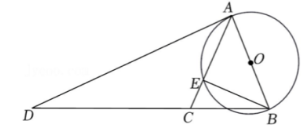
如图, 在 $\triangle A B C$ 中, $A B=A C$, 以 $A B$ 为直径作 $\odot O$ 与 $A C$ 交于点 $E$, 过点 $A$ 作 $\odot O$ 的切 线交 $B C$ 的延长线点 $D$.
(1) 求证: $\angle D=\angle E B C$;
(2) 若 $C D=2 B C, A E=6$, 求 $\frac{C E}{A B}$ 的值以及 $\odot O$ 的半径.
定义: 若一个函数图象上存在纵坐标是橫坐标 2 倍的点, 则把该函数称为 “青一函数”, 该点称为 “青一点”, 例如: “青一函数” $y=x+1$, 其 “青一点”为 $(1,2)$.
(1) ①判断: 函数 $y=2 x+3$ ( ) “青一函数” (填 “是”或 “不是”);
② 函数 $y=\frac{8}{x}$ 的图像上的青一点是 $ $
(2) 若抛物线 $y=(m-1) x^2+m x+\frac{1}{4} m$ 上有两个 “青一点”, 求 $m$ 的取值范围;
(3) 若函数 $y=x^2+(m-k+2) x+\frac{n}{4}-\frac{k}{2}$ 的图象上存在唯一的一个 “青一点”, 且当 $-1 \leqslant m \leqslant 3$ 时, $n$ 的最小值为 $k$, 求 $k$ 的值.
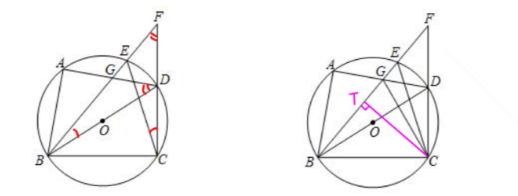
如图 1, 四边形 $A B C D$ 内接于以 $B D$ 为直径的 $\odot O, E$ 为 $\widehat{\mathrm{AD}}$ 上一点, 且 $\widehat{A E}=\widehat{\mathrm{CD}}$, 连结 $B E$ 并延长交 $C D$ 的延长线于点 $F, B E$ 与 $A D$ 交于点 $G$, 连接 $C E$.
(1) 求证: $A G \cdot B D=C D \cdot B G$;
(2) 若 $E F=\mathrm{D} G$. 求证: $A D=B G$.
(3) 如图 2, 在 (2) 的条件下, 连结 $C G, A D=4$, 求 $C G$ 的最小值.