单选题 (共 6 题 ),每题只有一个选项正确
已知 $\frac{(x+a y) \mathrm{d} x+y \mathrm{~d} y}{(x+y)^{2}}$ 为某函数的全微分, 则 $a$ 等于 ( )
$\text{A.}$ $-1$.
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ 2
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内连续,其导函数的图形如图所示, 则
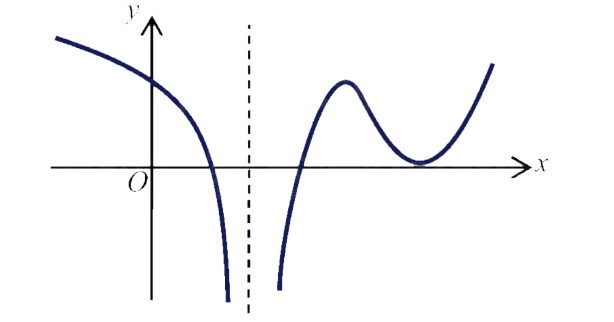
$\text{A.}$ 函数 $f(x)$ 有 2 个极值点,曲线 $y=f(x)$ 有 2 个拐点
$\text{B.}$ 函数 $f(x)$ 有 2 个极值点,曲线 $y=f(x)$ 有 3 个拐点
$\text{C.}$ 函数 $f(x)$ 有 3 个极值点,曲线 $y=f(x)$ 有 1 个拐点
$\text{D.}$ 函数 $f(x)$ 有 3 个极值点,曲线 $y=f(x)$ 有 2 个拐点
设函数 $f(x)=\left\{\begin{array}{l}-1, x < 0, \\ 1, x \geq 0,\end{array} \quad g(x)=\left\{\begin{array}{l}2-a x, x \leq-1, \\ x,-1 < x < 0, \\ x-b, x \geq 0 .\end{array}\right.\right.$
若 $f(x)+g(x)$ 在 $R$ 上连续,则
$\text{A.}$ $a=3, b=1$
$\text{B.}$ $a=3, b=2$
$\text{C.}$ $a=-3, b=1$
$\text{D.}$ $a=-3, b=2$
设 $M=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{(1+x)^2}{1+x^2} \mathrm{~d} x$,
$$
N=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1+x}{e^x} \mathrm{~d} x, K=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}(1+\sqrt{\cos x}) \mathrm{d} x ,
$$
则 $M, N, K$ 的大小关系为
$\text{A.}$ $M>N>K$
$\text{B.}$ $M>K>N$
$\text{C.}$ $K>M>N$
$\text{D.}$ $K>N>M$
设函数 $y=x \sin x+2 \cos x\left(-\frac{\pi}{2} < x < \frac{3 \pi}{2}\right)$ 的拐点坐标为
$\text{A.}$ $\left(\frac{\pi}{2}, \frac{\pi}{2}\right)$
$\text{B.}$ $(\pi,-2)$
$\text{C.}$ $(0,2)$
$\text{D.}$ $\left(\frac{3 \pi}{2}, \frac{3 \pi}{2}\right)$
$\int_0^1 \frac{\arcsin \sqrt{x}}{\sqrt{x(1-x)}} \mathrm{d} x=(\quad)$
$\text{A.}$ $\frac{\pi^2}{4}$
$\text{B.}$ $\frac{\pi^2}{8}$
$\text{C.}$ $\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{8}$