单选题 (共 2 题 ),每题只有一个选项正确
设 $\boldsymbol{A}$ 是 3 阶实对称矩阵, $\boldsymbol{E}$ 是 3 阶单位矩阵。若 $\boldsymbol{A}^2+\boldsymbol{A}=2 \boldsymbol{E}$ ,且 $|\boldsymbol{A}|=4$ ,则二次型 $\boldsymbol{x}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}$ 的规范形为()
$\text{A.}$ $y_1^2+y_2^2+y_3^2$.
$\text{B.}$ $y_1^2+y_2^2-y_3^2$.
$\text{C.}$ $y_1^2-y_2^2-y_3^2$.
$\text{D.}$ $-y_1^2-y_2^2-y_3^2$.
如图所示, 有 3 张平面两两相交, 交线相互平行, 它们的方程$a_{i 1} x+a_{i 2} y+a_{i 3} z=d_i(i=1,2,3)$ 组成的线性方程组的系数矩阵和增广矩阵分别记为 $\boldsymbol{A}, \overline{\boldsymbol{A}}$, 则
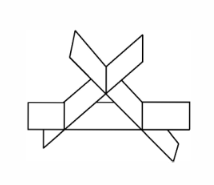
$\text{A.}$ $r(\boldsymbol{A})=2, r(\overline{\boldsymbol{A}})=3$.
$\text{B.}$ $r(\boldsymbol{A})=2, r(\overline{\boldsymbol{A}})=2$.
$\text{C.}$ $r(\boldsymbol{A})=1, r(\overline{\boldsymbol{A}})=2$.
$\text{D.}$ $r(\boldsymbol{A})=1, r(\overline{\boldsymbol{A}})=1$.
填空题 (共 1 题 ),请把答案直接填写在答题纸上
设 $\boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right)$ 为 3 阶矩阵。若 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2$ 线性无关,且 $\boldsymbol{\alpha}_3=-\boldsymbol{\alpha}_1+2 \boldsymbol{\alpha}_2$ ,则线性方程组 $\boldsymbol{A x}=\mathbf{0}$ 的通解为 $\qquad$ .
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设向量组
$$
\alpha_1=(1,2,1)^T, \alpha_2=(1,3,2)^T, \alpha_3=(1, a, 3)^T
$$
为 $R^3$ 的一组基,
$\beta=(1,1,1)^T$ 在这个基下的坐标为 $(b, c, 1)$.
(1) 求 $a, b, c$ 的值;
(2) 证明 $\alpha_2, \alpha_3, \beta$ 为 $R^3$ 的一组基,并求 $\alpha_2, \alpha_3, \beta$ 到 $\alpha_1, \alpha_2, \alpha_3$ 的过渡矩阵。
已知矩阵 $A=\left(\begin{array}{ccc}-2 & -2 & 1 \\ 2 & x & -2 \\ 0 & 0 & -2\end{array}\right)$ 与 $B=\left(\begin{array}{ccc}2 & 1 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & y\end{array}\right)$ 相似.
(1)求 $x, y$ ;
(2) 求可逆矩阵 $P$ ,使得 $P^{-1} A P=B$.