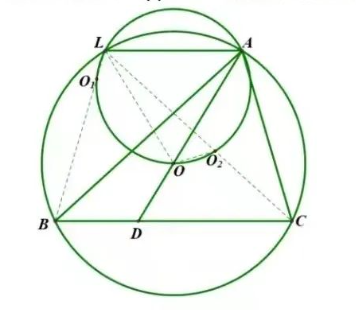
在锐角 $\triangle A B C$ 中, $A B>A C, O$ 为外心. 设 $D$ 为边 $B C$ 上一点, $O_1, O_2$ 分别为 $\triangle A B D$ 和 $\triangle A C D$ 的外心, $\triangle A O_1 O_2$ 的外接圆与 $\odot O$ 交于不同于点 $A$ 的点 $L$.
证明: $A, O, D$ 三点共线当且仅当 $A L / / B C$. (杨标桂供题)

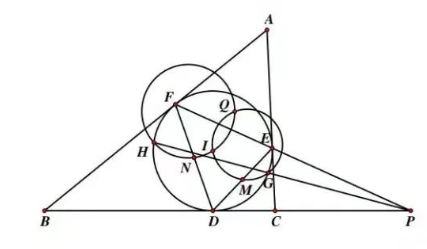
如图, 在 $\triangle A B C$ 中, $A B>A C, \triangle A B C$ 的内切圆 $I$ 分别切边 $B C, C A, A B$ 于点 $D, E, F$. 设 $M$ 为 $D E$ 中点, $N$ 为 $D F$ 中点, 直线 $F E$ 与 $B C$ 相交于点 $P$. 过点 $P$ 作动直线 $l$ 交内切圆 $I$ 于不同的两点 $G, H$, 且 $I, M, G$ 和 $I, N, H$ 均不共线, $\triangle I M G$ 的外接圆与 $\triangle I N H$ 的外接圆交于不同于 $I$ 的一点 $Q$. 证明: 点 $Q$ 始终在一个定圆上. (张惠东供题）