单选题 (共 6 题 ),每题只有一个选项正确
设函数 $f(x)=a(x+1)^2-1, g(x)=\cos x+2 a x$ ( $a$ 为常数), 当 $x \in(-1,1)$ 时, 曲线 $y=f(x)$ 与 $y=g(x)$恰有一个交点, 则 $a=$
$\text{A.}$ -1
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 1
$\text{D.}$ 2
已知实数 $x, y$ 满足 $e^x=y \ln x+y \ln y$, 则满足条件的 $\mathrm{y}$ 的最小正整数为
$\text{A.}$ 1
$\text{B.}$ 3
$\text{C.}$ 5
$\text{D.}$ 7
设函数 $f(x)=\frac{e^x+2 \sin x}{1+x^2}$, 则曲线 $y=f(x)$ 在点 $(0,1)$ 处的切线与坐标轴围成的三角形的面积为
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{2}{3}$
已知定义在 R 上的函数 $f(x)$ 满足 $2 f(x)=f(-x)+3 \mathrm{e}^x$, 则曲线 $y=f(x)$ 在点 $(0, f(0))$ 处的切线方程为
$\text{A.}$ $y=3 x+3$
$\text{B.}$ $y=3 x-3$
$\text{C.}$ $y=x+3$
$\text{D.}$ $y=x-3$
$\left(1 \frac{1}{2}\right)^0-\left(1-0.5^{-2}\right) \div \sqrt[3]{\left(\frac{27}{8}\right)^2}$ 的值为
$\text{A.}$ $-\frac{1}{3}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{4}{3}$
$\text{D.}$ $\frac{7}{3}$
如图是指数函数(1) $y=a^x$ ,(2) $y=b^x$ ,(3) $y=c^x ,$ (4) $y=d^x$ 的图像,则 $a , b , c , d$ 与 0 和1的大小关系是
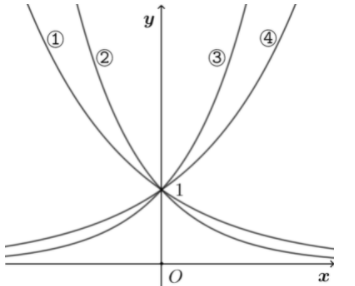
$\text{A.}$ $0 < a < b < 1 < c < d$
$\text{B.}$ $0 < b < a < 1 < d < c$
$\text{C.}$ $1 < a < b < c < d$
$\text{D.}$ $0 < a < b < 1 < d < c$