解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算定积分 $\int_0^{\frac{\pi}{2}} \frac{x+\sin x}{1+\cos x} d x$
设 $f(x), g(x)$ 在 $[a, b]$ 上二阶可导,且 $g^{\prime \prime}(x) \neq 0, f(a)=f(b)=g(a)=g(b)=0$,
证明:
(1) 在区间 $(a, b)$ 内 $g(x) \neq 0$,
(2) $\exists \xi \in(a, b)$, 使 $\frac{f(\xi)}{g(\xi)}=\frac{f^{\prime \prime}(\xi)}{g^{\prime \prime}(\xi)}$
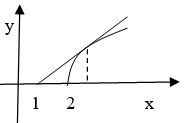
过点 $(1,0)$ 作抛物线 $y=\sqrt{x-2}$ 的切线. (1) 求该切线方程; (2) 求由这条切线、抛物线及 $x$ 轴所围成的平面图形面积; (3) 求 (2) 中平面图形绕 $x$ 轴旋转一周所得旋转体体积.
设函数 $f(x)$ 是满足初值问题 $\left\{\begin{array}{l}f^{\prime \prime}(x)+\left[f^{\prime}(x)\right]^2=x^2, \\ f(0)=a, f^{\prime}(0)=0\end{array}\right.$ 的特解, 试证明 $x=0$ 是 $y=f(x)$的极小值点.
设级数 $\sum_{n=1}^{\infty} a_n(x-1)^n$ 在点 $x=4$ 处条件收敛, 判断级数 $\sum_{n=1}^{\infty} a_n\left(1+\frac{1}{n}\right)^{n^2}$ 是否收敛, 若收敛,请说明是条件收敛,还是绝对收敛.
已知 $f(x)$ 在 $(-\infty,+\infty)$ 内可微, 且 $f(1)=f(-1)=1$, 若平面向量函数
$$
\boldsymbol{F}(x, y)=\frac{-x y^2}{y^4+f(x)} i+\frac{x^2 y}{y^4+f(x)} j
$$
是二元函数 $\Phi(x, y)$ 的梯度.
(I) 求函数 $f(x)$ 及 $\Phi(x, y)$;
( II ) 证明: $\oint_C \boldsymbol{F}(x, y) \cdot \mathrm{d} \boldsymbol{l}=0$, 其中 $C$ 是任意一条不通过 $\boldsymbol{F}(x, y)$ 的奇点 (使 $y^{\prime}+f(x)=0$的点) 的正向闭路径.