解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $f(x)$ 在 $[0,+\infty)$ 连续,广义积分 $\int_0^{+\infty} f(x) \mathrm{d} x$ 收敛. 证明:
$$
\lim _{\lambda \rightarrow 0^{+}} \int_0^{+\infty} e^{-\lambda x} f(x) \mathrm{d} x=\int_0^{+\infty} f(x) \mathrm{d} x .
$$
设
$
f(x, y)=\left\{\begin{array}{rr}
\left( x^2+y^2\right) \sin \frac{1}{x^2+y^2},(x, y) \neq(0,0) \\
0 ,(x, y)=(0,0)
\end{array} .\right.
$
证明:
(1) $f(x, y)$ 在 $(0,0)$ 处连续;
(2) $f(x, y)$ 在 $(0,0)$ 处存在偏导数;
(3) $f(x, y)$ 在 $(0,0)$ 处的偏导数不连续;
(4) $f(x, y)$ 在 $(0,0)$ 处可微.
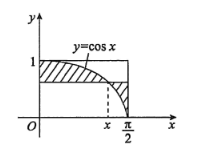
如图, 在 $\left(0, \frac{\pi}{2}\right)$ 内求一点 $x$, 使得阴影部分面积最小, 并求出该最小值.
设 $y=y(x)$ 为微分方程满足初值问题 $\left\{\begin{array}{l}\left(1-x^2\right) y^{\prime \prime}-x y^{\prime}=0, \\ y(0)=0, y^{\prime}(0)=1\end{array}\right.$ 的解, 求极限 $\lim _{x \rightarrow \frac{\sqrt{2}}{2}} \frac{y^2(x)-\frac{\pi^2}{16}}{2 x^2-1}$.
要制作一个中间为圆柱, 两端为相同的正圆雉的空浮标, 其体积为定值. 若要求用料最少, 求此时圆柱的高, 圆柱的半径和圆锥的高的比例.
求 $\iint_D|3 x+4 y| \mathrm{d} x \mathrm{~d} y$, 其中 $D=\left\{(x, y) \mid x^2+y^2 \leqslant 1\right\}$.