单选题 (共 10 题 ),每题只有一个选项正确
函数 $y=\frac{\sqrt{x}-2}{x-3}$ 的自变量 $x$ 的取值范围是
$\text{A.}$ $x \neq 3$
$\text{B.}$ $x>0$ 且 $x \neq 3$
$\text{C.}$ $x \geq 0$ 且 $x \neq 3$ 。
$\text{D.}$ $x>2$且 $x \neq 3$
已知实数 $a$ 满足 $|2022-a|+\sqrt{a-2023}=a$, 那么 $a-2022^2$ 的值是
$\text{A.}$ 2023
$\text{B.}$ 2022
$\text{C.}$ 2021
$\text{D.}$ 2020
实数 $a$ 在数轴上的对应位置如图所示, 则 $\sqrt{a^2}+1+|a-1|$ 的化简结果是
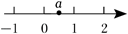
$\text{A.}$ $1$
$\text{B.}$ $2$
$\text{C.}$ $2 a$
$\text{D.}$ $1-2 a$
实数 $a, b$ 在数轴上的位置如图所示, 化简 $(\sqrt{a})^2+\sqrt{b^2}$ 的结果是
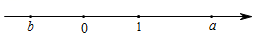
$\text{A.}$ $-a+b$
$\text{B.}$ $-a-b$
$\text{C.}$ $a+b$
$\text{D.}$ $a-b$
下列各式中是二次根式的为
$\text{A.}$ $a+b$
$\text{B.}$ $\frac{s}{t}$
$\text{C.}$ $-x^3$
$\text{D.}$ $\sqrt{a}(a \geq 0)$
代数式 $\frac{\sqrt{x}}{x-1}$ 有意义的条件是
$\text{A.}$ $x \neq 1$
$\text{B.}$ $x \geq 0$
$\text{C.}$ $x \geq 0$ 且 $x \neq 1$
$\text{D.}$ $0 \leq x \leq 1$
若 $\sqrt{x}+\sqrt{\frac{1}{x}}=\sqrt{6}, 0 < x < 1$, 则 $\sqrt{x}-\sqrt{\frac{1}{x}}$ 的值是
$\text{A.}$ $-\sqrt{2}$
$\text{B.}$ $-2$
$\text{C.}$ $\pm 2$
$\text{D.}$ $\pm \sqrt{2}$
在下列代数式中, 不是二次根式的是
$\text{A.}$ $\sqrt{5}$
$\text{B.}$ $\sqrt{\frac{1}{3}}$
$\text{C.}$ $\sqrt{x^2+1}$
$\text{D.}$ $\frac{2}{x}$
已知 $y=2 \sqrt{4 x-2}-3 \sqrt{4-8 x}+32$, 则 $\sqrt{x y}$ 的值为
$\text{A.}$ $\pm 4$
$\text{B.}$ $\pm 2$
$\text{C.}$ $ 4$
$\text{D.}$ $ 2$
已知 $x 、 y$ 为实数, 且 $y=\sqrt{x-2022}+\sqrt{2022-x}+3$, 则 $x+y$ 的值是
$\text{A.}$ 2022
$\text{B.}$ 2025
$\text{C.}$ 2027
$\text{D.}$ 2030
填空题 (共 5 题 ),请把答案直接填写在答题纸上
已知整数 $x, y$ 满足 $x \sqrt{y}+y \sqrt{x}-\sqrt{2022 x}-\sqrt{2022 y}+\sqrt{2022 x y}=2022$, 则 $\sqrt{x-y-7}$ 的最小值为
将 $x \sqrt{-\frac{6}{x^3}}$ 根号外的因式移到根号内:
设实数 $a 、 b$ 在数轴上对应的位置如图所示, 化简 $\sqrt{a^2-2 a b+b^2}+|a+b|$ 的结果是

已知 $a, b$ 都是实数, $b=\sqrt{1-2 a}+\sqrt{4 a-2}-2$, 则 $a^b$ 的值为
若 $x 、 y$ 都为实数, 且 $y=2022 \sqrt{x-4}+2022 \sqrt{4-x}+9$, 则 $x y$ 的值
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
阅读材料并解决下列问题:
已知 $a 、 b$ 是有理数, 并且满足等式 $5-\sqrt{3} a=2 b+\frac{2}{3} \sqrt{3}-a$, 求 $a 、 b$ 的值.
解: $\because 5-\sqrt{3} a=2 b+\frac{2}{3} \sqrt{3}-a$
即 $5-\sqrt{3} a=(2 b-a)+\frac{2}{3} \sqrt{3}$
$$
\therefore 2 b-a=5,-a=\frac{2}{3}
$$
解得: $a=-\frac{2}{3}, b=\frac{13}{6}$
(1) 已知 $a 、 b$ 是有理数, 并且满足等式 $\sqrt{2} a-(1+\sqrt{2}) b=3 \sqrt{2}-1$, 则 $a=, b=$
(2) 已知 $x 、 y$ 是有理数, 并且满足等式 $x+\sqrt{5} y+2 y-2 \sqrt{5}=3 \sqrt{5} x+18$, 求 $x y$ 的平方根.
已知 $a$ 满足 $|2021-a|+\sqrt{a-2022}=a$.
(1) $\sqrt{a-2022}$ 有意义, $a$ 的取值范围是 ; 则在这个条件下将 $2021-a \mid$ 去掉绝对值符 号可得 $|2021-a|=$
(2)根据 (1) 的分析, 求 $a-2021^2$ 的值.
小颖利用平方差公式, 自己探究出一种解某一类根式方程的方法. 下面是她解方程 $\sqrt{x-2}+\sqrt{x-7}=5$ 的过程.
解: 设 $\sqrt{x-2}-\sqrt{x-7}=m$, 与原方程相乘得:
$$
\begin{aligned}
& (\sqrt{x-2}+\sqrt{x-7}) \times(\sqrt{x-2}-\sqrt{x-7})=5 m, \\
& x-2-(x-7)=5 m \text {, 解之得 } m=1, \\
& \therefore \sqrt{x-2}-\sqrt{x-7}=1 \text {, 与原方程相加得: } \\
& (\sqrt{x-2}+\sqrt{x-7})+(\sqrt{x-2}-\sqrt{x-7})=5+1,
\end{aligned}
$$
$2 \sqrt{x-2}=6$, 解之得, $x=11$, 经检验, $x=11$ 是原方程的根.
学习借鉴解法, 解方程 $\sqrt{x-3}-\sqrt{x-6}=1$.
当 $a=2022$ 时, 求 $a+\sqrt{a^2-2 a+1}$ 的值. 如图是小亮和小芳的解答过程:

(1) ( ) 的解法是错误的;
(2)错误的原因在于末能正确地运用二次根式的性质 ( )
(3)当 $a>3$ 时, 求 $\sqrt{a^2-6 a+9}-|1-a|$ 的值.