单选题 (共 12 题 ),每题只有一个选项正确
设集合 $A=\{x \mid-1 < x \leqslant 2\}, B=\left\{x \mid x^2-4 x+3 \leqslant 0\right\}$, 则 $A \cap B=$
$\text{A.}$ $\{x \mid-1 < x \leqslant 3\}$
$\text{B.}$ $\{x \mid-1 < x \leqslant 1\}$
$\text{C.}$ $\{x \mid 1 \leqslant x \leqslant 2\}$
$\text{D.}$ $\{x \mid 1 \leqslant x \leqslant 3\}$
满足 $(1+\mathrm{i}) z=3+\mathrm{i}(\mathrm{i}$ 为虚数单位 $)$ 的复数 $z=$
$\text{A.}$ $2-\mathrm{i}$
$\text{B.}$ $2+\mathrm{i}$
$\text{C.}$ $1+2 \mathrm{i}$
$\text{D.}$ $1-2 \mathrm{i}$
抛物线 $x^2=2 y$ 的焦点坐标为
$\text{A.}$ $(0,1)$
$\text{B.}$ $\left(0, \frac{1}{2}\right)$
$\text{C.}$ $\left(\frac{1}{4}, 0\right)$
$\text{D.}$ $\left(\frac{1}{8}, 0\right)$
下图为 2012 年一2021 年我国电子信息制造业企业和工业企业利润总额增速情况折线图.

根据该图, 下列结论正确的是
$\text{A.}$ 2012 年一2021 年电子信息制造业企业利润总额逐年递增
$\text{B.}$ 2012 年一2021 年工业企业利润总额逐年递增
$\text{C.}$ 2012 年一2017 年电子信息制造业企业利润总额均较上一年实现增长, 且其增速均快 于当年工业企业利润总额增速
$\text{D.}$ 2012 年一2021 年工业企业利润总额增速的均值大于电子信息制造业企业利润总额增 速的均值
若实数 $x, y$ 满足约束条件 $\left\{\begin{array}{l}x+y-4 \leqslant 0, \\ y \geqslant y \geqslant 0 .\end{array} \quad\right.$ 则 $z=x+2 y$ 的最大值是
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 7
若圆雉的侧面展开图为一个半圆面, 则它的底面面积与侧面面积之比是
$\text{A.}$ $\sqrt{2}: 1$
$\text{B.}$ $2: 1$
$\text{C.}$ $1: \sqrt{2}$
$\text{D.}$ $1: 2$
下列命题中错误的是
$\text{A.}$ 在回归分析中, 相关系数 $r$ 的绝对值越大, 两个变量的线性相关性越强
$\text{B.}$ 对分类变量 $X$ 与 $Y$, 它们的随机变量 $K^2$ 的观测值 $k$ 越小, 说明 “ $X$ 与 $Y$ 有关系”的把 握越大
$\text{C.}$ 线性回归直线 $\hat{y}=\hat{b} x+\hat{a}$ 恒过样本中心 $(\bar{x}, \bar{y})$
$\text{D.}$ 在回归分析中, 残差平方和越小, 模型的拟合效果越好
若函数 $f(x)=x^3+2 a x^2+a^2 x$ 在 $x=1$ 处有极大值, 则实数 $a$ 的值为
$\text{A.}$ $ 1$
$\text{B.}$ $-1$ 或 $-3$
$\text{C.}$ $-1$
$\text{D.}$ $-3$
已知直线 $l, m$ 和平面 $\alpha, \beta$. 若 $\alpha \perp \beta, l \perp \alpha$, 则 “ $l \perp m$ ” 是 “ $m \perp \beta$ ”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$. 若 $a_1=2, a_{n+1}=S_n$, 则 $S_8=$
$\text{A.}$ 512
$\text{B.}$ 510
$\text{C.}$ 256
$\text{D.}$ 254
日光射人海水后, 一部分被海水吸收 (变为热能), 同时, 另一部分被海水中的有机物和无机 物有选择性地吸收与散射. 因而海水中的光照强度随着深度增加而减弱, 可用 $I_D=I_0 \mathrm{e}^{-K D}$ 表示其总衰减规律, 其中 $K$ 是平均消光系数 (也称衰减系数), $D$ (单位: 米) 是海水深度, $I_D$ (单位:坎德拉) 和 $I_0$ (单位: 坎德拉) 分别表示在深度 $D$ 处和海面的光强. 已知某海区 10 米 深处的光强是海面光强的 $30 \%$, 则该海区消光系数 $K$ 的值约为 (参考数据: $\ln 2 \approx 0.7$, $\ln 3 \approx 1.1, \ln 5 \approx 1.6$ )
$\text{A.}$ $0.12$
$\text{B.}$ $0.11$
$\text{C.}$ $0.07$
$\text{D.}$ $0.01$
已知侧棱长为 $2 \sqrt{3}$ 的正四棱雉各顶点都在同一球面上. 若该球的表面积为 $36 \pi$, 则该正四 棱雉的体积为
$\text{A.}$ $\frac{16}{3}$
$\text{B.}$ $\frac{8 \sqrt{2}}{3}$
$\text{C.}$ $\frac{8}{3}$
$\text{D.}$ $\frac{32}{3}$
填空题 (共 11 题 ),请把答案直接填写在答题纸上
在公差为 $d$ 的等差数列 $\left\{a_n\right\}$ 中, 已知 $a_1+a_2+a_3=3, a_4+a_6=4$, 则 $d=$
已知双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的渐近线与圆 $x^2+y^2-4 y+3=0$ 相切, 则双曲线的 离心率为
已知平面向量 $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}$ 满足 $|\boldsymbol{a}|=|\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|=1, \boldsymbol{c} \cdot \boldsymbol{a}=\boldsymbol{c} \cdot \boldsymbol{b}=1$, 则 $|\boldsymbol{c}|=$
已知函数 $f(x)=\sin ^2 x-\sin x+k, x \in[0, \pi]$. 有下列结论:
(1) 若函数 $f(x)$ 有零点,则 $k$ 的取值范围是 $\left(-\infty, \frac{1}{4}\right]$;
(2)若 $k=\frac{1}{4}$, 则函数 $f(x)$ 的零点为 $\frac{\pi}{6}, \frac{5 \pi}{6}$;
(3) 函数 $f(x)$ 的零点个数可能为 $0,2,3,4$;
(4)若函数 $f(x)$ 有四个零点 $x_1, x_2, x_3, x_4$, 则 $k \in\left(0, \frac{1}{4}\right)$, 且 $x_1+x_2+x_3+x_4=2 \pi$.
其中所有正确结论的编号为
成都作为常住人口超 2000 万的超大城市, 注册青年志愿者人数超 114 万, 志愿服务时长超 268 万小时. 2022 年 6 月, 成都 22 个市级部门联合启动了 2022 年成都市青年志愿服务项目大赛, 项目大赛申报期间, 共收到 331 个主体的 416 个志愿服务项目, 覆盖文明实践、社区治理与邻里 守望、环境保护等 13 大领域. 已知某领域共有 50 支志愿队伍申报, 主管部门组织专家对志愿者 申报队伍进行评审打分, 并将专家评分(单位: 分) 分成 6 组: $[40,50),[50,60), \cdots,[90,100]$, 得 到如图所示的频率分布直方图.
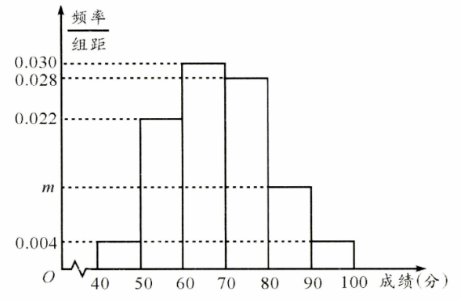
(I) 求图中 $m$ 的值;
(II) 已知评分在 $[85,100]$ 的队伍有 4 支, 若从评分在 [80, 90) 的队伍中任选 两支队伍, 求这两支队伍至少有一支队 伍评分不低于 85 分的概率.
记 $\triangle A B C$ 的内角 $A, B, C$ 所对边分别为 $a, b, c$. 已知 $\frac{b}{a}=\sin C+\cos C$.
( I ) 求 $A$ 的大小;
(II) 若 $2 \sqrt{2} \sin B=3 \sin C$, 再从下列条件(1), 条件(2)中任选一个作为已知, 求 $\triangle A B C$ 的面积. 条件(1): $a \sin C=2$; 条件(2) $a c=2 \sqrt{10}$.
注: 如果选择多个条件分别解答, 按第一个解答计分.
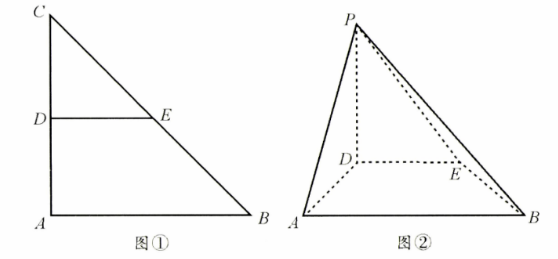
如图(1), 在等腰直角三角形 $A B C$ 中, $\angle A=90^{\circ}, A B=2, D, E$ 分别是 $A C, B C$ 上的点, 且 满足 $D E / / A B$. 将 $\triangle C D E$ 沿 $D E$ 折起, 得到如图(2)所示的四棱雉 $P-A B E D$.
( I) 若 $D$ 为 $A C$ 的中点, 平面 $P D E \perp$ 平面 $A B E D$, 求四棱雉 $P-A B E D$ 的体积;
( II ) 设平面 $A B P \cap$ 平面 $D E P=l$, 证明: $l \perp$ 平面 $A D P$.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左, 右焦点分别为 $F_1, F_2$, 上顶点为 $D$, 且 $\triangle D F_1 F_2$ 为等边三角形. 经过焦点 $F_2$ 的直线 $l$ 与椭圆 $C$ 相交于 $A, B$ 两点, $\triangle F_1 A B$ 的周长为 8 .
(I) 求椭圆 $C$ 的方程;
(II) 求 $\triangle F_1 A B$ 的面积的最大值及此时直线 $l$ 的方程.
已知函数 $f(x)=\ln x+a-1, a \in \mathbf{R}$.
(I) 若 $f(x) \leqslant x$, 求 $a$ 的取值范围;
(II) 当 $a \in(0,1]$ 时, 证明: $f(x) \leqslant \frac{(x-1) \mathrm{e}^x}{\mathrm{e}^a}$.
在直角坐标系 $x O y$ 中, 圆心为 $A$ 的圆 $C_1$ 的参数方程为 $\left\{\begin{array}{l}x=2+\cos t, \\ y=\sin t\end{array}\right.$ ( $t$ 为参数). 以坐 标原点 $O$ 为极点, $x$ 轴正半轴为极轴建立极坐标系, 曲线 $C_2$ 的极坐标方程为 $\rho=2-2 \cos \theta$.
( I) 求圆 $C_1$ 的极坐标方程;
(II) 设点 $B$ 在曲线 $C_2$ 上, 且满足 $|A B|=\sqrt{3}$, 求点 $B$ 的极径.
选修 4-5: 不等式选讲 已知 $a, b$ 为非负实数, 函数 $f(x)=|x-3 a|+|x+4 b|$.
(I) 当 $a=1, b=\frac{1}{2}$ 时, 解不等式 $f(x) \geqslant 7$;
(II) 若函数 $f(x)$ 的最小值为 6 , 求 $\sqrt{3 a}+\sqrt{b}$ 的最大值.