单选题 (共 8 题 ),每题只有一个选项正确
在真空中波长为 $\lambda$ 的单色光,在折射率为 $n$ 的透明介质中从 $A$ 沿某路径传播到 $B$, 若 $A 、 B$ 两点相位差为 $3 \pi$, 则此路 径 $A B$ 的光程为
$\text{A.}$ $1.5 \lambda$
$\text{B.}$ $1.5^{\lambda / n}$
$\text{C.}$ $1.5 n^\lambda$
$\text{D.}$ $3 \lambda$
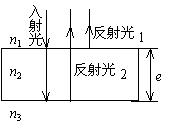
单色平行光垂直照射在薄膜上,经上下两表面反射的两束光发生干涉,如图所示,若薄膜的厚度为 $e ,$ 且 $n_1 < n_2>n_3$ , $\lambda_1$ 为入射光在 $n_1$ 中的波长,则两束反射光的光程差为
$\text{A.}$ $2 n_2 e$.
$\text{B.}$ $2 n_2 e-\lambda_1 /\left(2 n_1\right)$
$\text{C.}$ $2 n_2 e-n_1 \lambda_1 / 2$
$\text{D.}$ $2 n_2 e-n_2 \lambda_1 / 2$
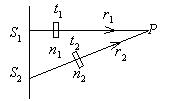
如图, $S_1 、 S_2$ 是两个相干光源, 它们到 $P$ 点的距离分别为 $r_1$ 和 $r_2$. 路径 $S_1 P$ 垂直穿过一块厚度为 $t_1$, 折射率为 $n_1$ 的介质 板,路径 $S_2 \mathrm{P}$ 垂直穿过厚度为 $t_2$, 折射率为 $n_2$ 的另一介质板, 其余部分可看作真空, 这两条路径的光程差等于+
$\text{A.}$ $\left(r_2+n_2 t_2\right)-\left(r_1+n_1 t_1\right)$
$\text{B.}$ $\left[r_2+\left(n_2-1\right) t_2\right]-\left[r_1+\left(n_1-1\right) t_2\right]$
$\text{C.}$ $\left(r_2-n_2 t_2\right)-\left(r_1-n_1 t_1\right)$
$\text{D.}$ $n_2 t_2-n_1 t_1$
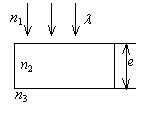
如图所示,波长为 $\lambda$ 的平行单色光垂直入射在折射率为 $n_2$ 的薄膜上,经上下两个表面反射的两束光发生干涉.若薄膜厚 度为 $e$, 而且 $n_1>n_2>n_3$, 则两束反射光在相遇点的相位差为
$\text{A.}$ $4 \pi n_2 e / \lambda$
$\text{B.}$ $2 \pi n_2 e / \lambda$
$\text{C.}$ $\left(4 \pi n_2 e / \lambda\right)+\pi$
$\text{D.}$ $\left(2 \pi n_2 e / \lambda\right)-\pi$
在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是
$\text{A.}$ 使屏靠近双缝 .
$\text{B.}$ 使两缝的间距变小.
$\text{C.}$ 把两个缝的宽度稍微调窄。
$\text{D.}$ 改用波长较小的单色光源 .
在双缝干涉实验中,两缝间距为 $d$ ,双缝与屏幕的距离为 $D(D \gg d)$, 单色光波长为 $\lambda$, 屏幕上相邻明条纹之间的 距离为
$\text{A.}$ $\lambda D / d$
$\text{B.}$ $\lambda d / D$
$\text{C.}$ $^{\lambda D /(2 d)}$
$\text{D.}$ $^{\lambda d /(2 D)}$
在单缝夫琅禾费衍射实验中,波长为 $\lambda$ 的单色光垂直入射在宽度为 $a=4^\lambda$ 的单缝上,对应于衍射角为 $30^{\circ}$ 的方向,单 缝处波阵面可分成的半波带数目为
$\text{A.}$ 2 个.
$\text{B.}$ 4个.
$\text{C.}$ 6个.
$\text{D.}$ 8个.
使一光强为 $I_0$ 的平面偏振光先后通过两个偏振片 $P_1$ 和 $P_2 . P_1$ 和 $P_2$ 的偏振化方向与原入射光光矢量振动方向的夹角分 别是 $\alpha$ 和 $90^{\circ}$, 则通过这两个偏振片后的光强 $I$ 是
$\text{A.}$ $\frac{1}{2} I_0 \cos ^2 \alpha$.
$\text{B.}$ 0
$\text{C.}$ ${\frac{1}{4}}{I_0 \sin ^2(2} \alpha)$.
$\text{D.}$ $\frac{1}{4}{I_0 \sin ^2} \alpha$.
填空题 (共 3 题 ),请把答案直接填写在答题纸上
若一双封装置的两个缝分别被折射率为 $n_1$ 和 $n_2$ 的两块厚度均为 $e$ 的透明介质所遮盖,此时由双缝分别到屏上原中央极 大所在处的两束光的光程差 $\delta=$
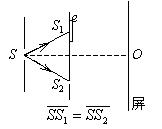
如图,在双缝干涉实验中,若把一厚度为 $e 、$ 折射率为 $n$ 的薄云母片覆盖在 $S_1$ 缝上,中央明条纹将向 ________ 移动;覆盖云母 片后, 两束相干光至原中央明纹 $O$ 处的光程差为 ________
在单缝夫琅禾费衍射实验中波长为 $\lambda$ 的单色光垂直入射在宽度为 $a=2 \lambda$ 的单缝上, 对应于衍射角为 $30^{\circ}$ 方向, 单缝处 的波面可分成的半波带数目为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在牛顿环装置的平凸透镜和平玻璃板之间充以折射率 $n=1.33$ 的液体(透镜和平玻璃板的折射率都大于 1.33 ). 凸透 镜曲率半径为 $300 \mathrm{~cm}$, 用波长 $\lambda=650 \mathrm{~nm}(1 \mathrm{~nm}=10-9 \mathrm{~m}$ ) 的光垂直照射, 求第 10 个暗环的半径( 设凸透镜中心刚好与平 板接触, 中心暗斑不计入环数)。
在用钠光 $(\lambda=589.3 \mathrm{~nm})$ 做光源进行的单缝夫琅禾费衍射实验中, 单缝宽度 $a=0.5 \mathrm{~mm}$ ,透镜焦距 $f=700 \mathrm{~mm}$. 求透镜焦 平面上中央明条纹的宽度 . $(1 \mathrm{~nm}=10-9 \mathrm{~m})$
在单缝的夫琅禾费衍射中, 缝宽 $a=0.100 \mathrm{~mm}$, 平行光垂直入射在单缝上, 波长 $\lambda=500 \mathrm{~nm}$, 会聚透镜的焦距 $f=1.00$ $\mathrm{m}$. 求中央亮纹旁的第一个亮纹的宽度 $\Delta_x$.
两个偏振片叠在一起,在它们的偏振化方向成 $\alpha_1=30^{\circ}$ 时,观测一束单色自然光. 又在 $\alpha_2=45^{\circ}$ 时,观测另一束单色自 然光. 若两次所测得的透射光强度相等, 求两次入射自然光的强度之比。
波长 $\lambda=600 \mathrm{~nm}\left(1 \mathrm{~nm}=10^{-} \mathrm{m}\right)$ 的单色光垂直入射到一光栅上, 测得第二级主极大的衍射角为 $30^{\circ}$, 且第三级是缺级.
$(1)$ 光栅常数 $(a+b)$ 等于多少?
(2)透光谜可能的最小宽度 $a$ 等于多少?
(3)在选定了上述 $(a+b)$ 和 $a$ 之后, 求在衍射角$-\frac{1}{2} \pi < \varphi < \frac{1}{2} \pi$ 范围内可能观察到的全部主极大的级次.