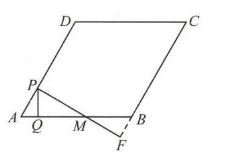
如图, 在菱形 $A B C D$ 中, $A B=4, \angle B A D=60^{\circ}$, 点 $P$ 从点 $A$ 出发, 沿线段 $A D$ 以每 秒 1 个单位长度的速度向终点 $D$ 运动, 过点 $P$ 作 $P Q \perp A B$ 于点 $Q$, 作 $P M \perp A D$ 交直线 $A B$ 于点 $M$, 交直线 $B C$ 于点 $F$, 设 $\triangle P Q M$ 与菱形 $A B C D$ 重叠部分图形的面积为 $S$ (平方单位), 点 $P$ 运动时间为 $t$ (秒) .
(1) 当点 $M$ 与点 $B$ 重合时, 求 $t$ 的值;
(2) 当 $t$ 为何值时, $\triangle A P Q$ 与 $\triangle B M F$ 全等;
(3) 求 $S$ 与 $t$ 的函数关系式;
(4) 以线段 $P Q$ 为边, 在 $P Q$ 右侧作等边三角形 $P Q E$, 当 $2 \leqslant t \leqslant 4$ 时, 请直接写出点 $E$ 运动路径的长.

如图 , 抛物线 $C_1: y=x^2+2 x+c$ 与拋物线 $C_2: y=x^2-4 x+d$ 相交于点 $T$, 点 $T$ 的横坐标 为 1. 过点 $T$ 作 $x$ 轴的平行线交抛物线 $C_1$ 于点 $A$, 交抛物线 $C_2$ 于点 $B$. 抛物线 $C_1$ 与 $C_2$ 分别与 $\mathrm{y}$ 轴交于点 $\mathrm{C}, \mathrm{D}$.
(1)求抛物线 $\mathrm{C}_1$ 的对称轴和点 $\mathrm{A}$ 的横坐标,并求线段 $\mathrm{AB}$ 的长;
(2) 点 $P(-2, p)$ 在抛物线 $C_1$ 上,点 $Q(5, q)$ 在抛物线 $C_2$ 上,则 $\mathrm{p}$ （　　） $q$ ( 填 $ > < =$)
(3) 若点 $C(0,-1)$, 求将抛物线 $C_1$ 平移到拋物线 $C_2$ 的最短距离.