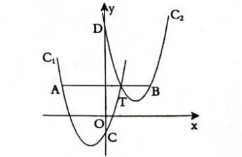
如图 , 抛物线 $C_1: y=x^2+2 x+c$ 与拋物线 $C_2: y=x^2-4 x+d$ 相交于点 $T$, 点 $T$ 的横坐标 为 1. 过点 $T$ 作 $x$ 轴的平行线交抛物线 $C_1$ 于点 $A$, 交抛物线 $C_2$ 于点 $B$. 抛物线 $C_1$ 与 $C_2$ 分别与 $\mathrm{y}$ 轴交于点 $\mathrm{C}, \mathrm{D}$.
(1)求抛物线 $\mathrm{C}_1$ 的对称轴和点 $\mathrm{A}$ 的横坐标,并求线段 $\mathrm{AB}$ 的长;
(2) 点 $P(-2, p)$ 在抛物线 $C_1$ 上,点 $Q(5, q)$ 在抛物线 $C_2$ 上,则 $\mathrm{p}$ （　　） $q$ ( 填 $ > < =$)
(3) 若点 $C(0,-1)$, 求将抛物线 $C_1$ 平移到拋物线 $C_2$ 的最短距离.