多选题 (共 2 题 ),每题有多个选项正确
圆心为 $O$ 、半径为 $R$ 的圆形区域内存在磁感应强度大小为 $B$ 、方向垂直纸面的匀强磁场(未画出),磁场边缘上的 $A$ 点有一带正电粒子源,半径 $O A$ 坚直,$M N$ 与 $O A$ 平行,且与圆形边界相切于 $B$ 点,在 $M N$ 的右侧有范围足够大且水平向左的匀强电场,电场强度大小为 $E$ 。当粒子的速度大小为 $v_0$ 且沿 $A O$ 方向时,粒子刚好从 $B$ 点离开磁场,不计粒子重力和粒子间的相互作用,下列说法正确的是

$\text{A.}$ 圆形区域内磁场方向垂直纸面向外
$\text{B.}$ 粒子的比荷为 $\frac{v_0}{B R}$
$\text{C.}$ 粒子在磁场中运动的总时间为 $\frac{\pi R}{2 v_0}$
$\text{D.}$ 粒子在电场中运动的总时间为 $\frac{2 B R}{E}$
如图所示的平面直角坐标系 $x O y$ ,在 $y$ 轴的左侧存在沿 $y$ 轴负方向的匀强电场。在 $y$ 轴的右侧存在垂直坐标平面向外的匀强磁场。
一比荷为 $k$ 的带正电粒子(不计重力)从 $x$ 轴上的 $A$ 点以沿着与 $x$ 轴正方向成 $\theta$ $=53^{\circ}$ 角的初速度 $v_0$ 开始运动,经过电场偏转从 $y$ 轴的 $B$ 点以垂直 $y$ 轴的速度进入磁场,磁场的磁感应强度大小为 $\frac{3 v_0}{5 k d}$ 粒子进入磁场后电场方向变为沿 $y$ 轴正方向.该带正电粒子经过磁场偏转,粒子先后经过 $x$ 轴上的 $C$ 点、 $y$ 轴上的 $D$ 点,粒子经 $D$ 点后,再次回到 $x$ 轴上的 $A$ 点, $\sin 53^{\circ}$ $=\frac{4}{5}, \cos 53^{\circ}=\frac{3}{5}$

下列说法正确的是
$\text{A.}$ 粒子在磁场中做匀速圆周运动的轨迹半径为 $d$
$\text{B.}$ $A 、 C$ 两点之间的距离为 $3 d$
$\text{C.}$ 匀强电场的电场强度为 $\frac{4 v_0{ }^2}{5 k d}$
$\text{D.}$ 粒子从 $A$ 点开始到再回到 $A$ 点的运动时间为 $\frac{(15+5 \pi) d}{3 v_0}$
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
平面直角坐标系 $x O y$ 中,第二象限存在沿 $y$ 轴负方向的匀强电场,电场强度大小为 $E$ ,第三、四象限存在垂直坐标平面向里的匀强磁场,如图所示.一质量为 $m$ 、带电荷量为 $q$ 的正粒子从坐标为 $(-L, L)$ 的 $P$ 点沿 $y$ 轴负方向进入电场,初速度大小为 $v_0=\sqrt{\frac{2 E q L}{m} \text { ,粒子第二次到达 } x \text { 轴的位置为 }}$坐标原点.不计粒子的重力.
(1)求匀强磁场的磁感应强度 $B$ 的大小;
(2)若粒子由 $P$ 点沿 $x$ 轴正方向入射,初速度仍为 $v_0=\sqrt{\frac{2 E q L}{m}}$ ,求粒子第二次到达 $x$ 轴时与坐标原点的距离.
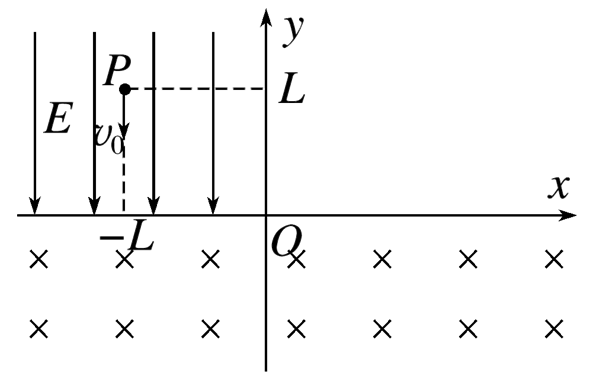
如图所示,$x O y$ 平面内,$O P$ 与 $x$ 轴正方向的夹角为 $\theta=53^{\circ}$ ,在 $x O P$ 范围内(含边界)存在垂直于坐标平面向里的匀强磁场,磁感应强度大小为 $B=$ 0.1 T .第二象限有平行于 $y$ 轴向下的匀强电场,电场强度大小为 $E=\frac{83}{40} \times$ $10^5 V / m$ .一带电微粒以速度 $v_0=5 \times 10^6 m / s$ 从 $x$ 轴上 $a(L, 0)$ 点平行于 $O P$ 射入磁场,并从 $O P$ 上的 $b$ 点垂直于 $O P$ 离开磁场,与 $y$ 轴交于 $c$ 点,最后回到 $x$ 轴上的 $d$ 点,图中 $b 、 d$ 两点未标出.已知 $L=\frac{5}{4} m$ , $\sin 53^{\circ}=\frac{4}{5}, \cos 53^{\circ}=\frac{3}{5}$ ,不计微粒的重力,求:

(1)微粒的比荷 $\frac{q}{m}$ ;
(2)d点与O点的距离l;
(3)仅改变磁场强弱而其他条件不变,当磁感应强度Bx大小满足什么条件时,微粒能到达第四象限.
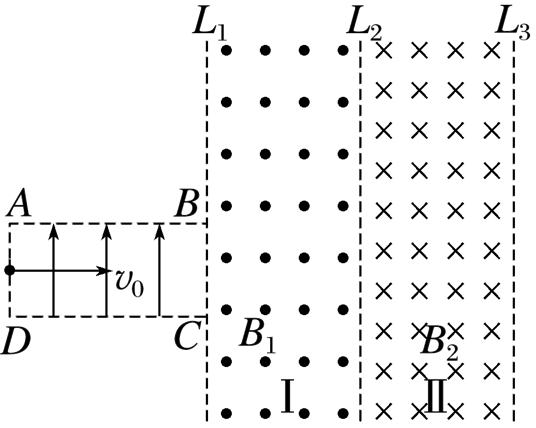
如图所示,在矩形区域 $A B C D$ 内存在竖直向上的匀强电场,在 $B C$ 右侧 I、II 两区域存在匀强磁场,$L_1 、 L_2 、 L_3$ 是磁场的边界( $B C$ 与 $L_1$ 重合),宽度相等,方向如图所示,区域 I 的磁感应强度大小为 $B_1$ 。一电荷量为 $+q$ 、质量为 $m$ 的粒子(重力不计)从 $A D$ 边中点以初速度 $v_0$ 沿水平向右方向进入电场,粒子恰好从 $B$ 点进入磁场,经区域 $I$ 后又恰好从与 $B$ 点同一水平高度处进入区域 II.已知 $A B$ 长度是 $B C$ 长度的 $\sqrt{3}$ 倍.
(1)求带电粒子到达 $B$ 点时的速度大小;
(2)求区域Ⅰ磁场的宽度L;
(3) 要使带电粒子在整个磁场中运动的时间最长,求区域Ⅱ中的磁感应强度B2的最小值.
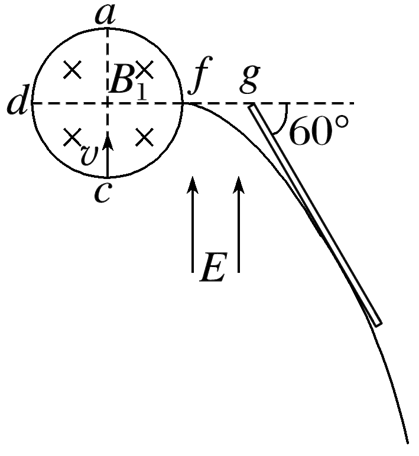
如图所示,半径为 $R$ 的圆形区域内存在垂直纸面向里的匀强磁场,圆形区域内 $a c 、 d f$ 为互相垂直的坚直和水平两条直径,沿 $d f$ 方向距 $f$ 点为 $R$ 的 $g$ 点处固定一足够长的挡板,挡板与 $f g$ 方向的夹角 $\alpha$ $=60^{\circ}$ ,粒子打到挡板上会被吸收,圆形磁场区域以外空间存在竖直向上的匀强电场。一质量为 $m$ 、电荷量为 $q$ 的带负电粒子(不计重力)自 $c$ 点沿 $c a$ 方向以速度 $v$ 射入磁场,经磁场偏转后从 $f$ 点沿 $f g$
方向射出磁场,之后恰好未打在挡板上,图中已画出粒子在电场中运动的轨迹.
(1)求匀强磁场的磁感应强度大小 $B_1$ ;
(2)求匀强电场的电场强度大小E;
(3)若将原电场换为方向垂直纸面向里的匀强磁场,其磁感应强度大小B2=kB1(0 < k≤1),求粒子返回圆形磁场区域边界时的位置到f点的距离.