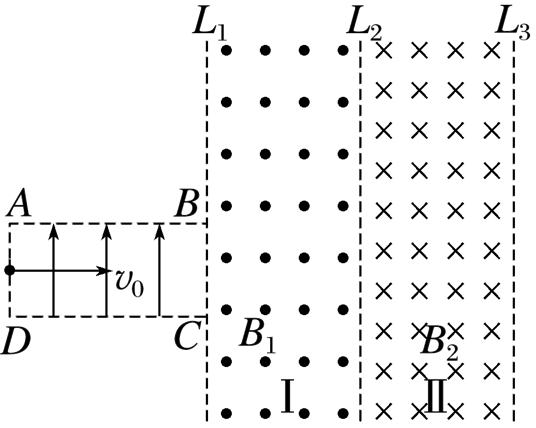
如图所示，在矩形区域 $A B C D$ 内存在竖直向上的匀强电场，在 $B C$ 右侧 I、II 两区域存在匀强磁场，$L_1 、 L_2 、 L_3$ 是磁场的边界（ $B C$ 与 $L_1$ 重合），宽度相等，方向如图所示，区域 I 的磁感应强度大小为 $B_1$ 。一电荷量为 $+q$ 、质量为 $m$ 的粒子（重力不计）从 $A D$ 边中点以初速度 $v_0$ 沿水平向右方向进入电场，粒子恰好从 $B$ 点进入磁场，经区域 $I$ 后又恰好从与 $B$ 点同一水平高度处进入区域 II．已知 $A B$ 长度是 $B C$ 长度的 $\sqrt{3}$ 倍．
（1）求带电粒子到达 $B$ 点时的速度大小；
（2）求区域Ⅰ磁场的宽度L；
(3) 要使带电粒子在整个磁场中运动的时间最长，求区域Ⅱ中的磁感应强度B2的最小值.