单选题 （共 10 题 ），每题只有一个选项正确
若 $\alpha$ 是第四象限角，则 $\pi+\alpha$ 是第 $\qquad$象限角（
$\text{A.}$ 一
$\text{B.}$ 二
$\text{C.}$ 三
$\text{D.}$ 四
已知角 $\theta$ 的终边经过点 $P\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)$ ，则角 $\theta$ 可以为（
$\text{A.}$ $\frac{5 \pi}{6}$
$\text{B.}$ $\frac{2 \pi}{3}$
$\text{C.}$ $\frac{11 \pi}{6}$
$\text{D.}$ $\frac{5 \pi}{3}$
中国折叠扇有着深厚的文化底蕴．如图，在半圆 $O$ 中作出两个扇形$OAB$ 和 $O C D$ ，用扇环形 $A B D C$（图中阴影部分）制作折叠扇的扇面．记扇环形 $A B D C$ 的面积为 $S_{1}$ ，扇形
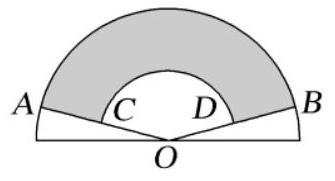
$O A B$ 的面积为 $S_{2}$ ，当 $S_{1}$ 与 $S_{2}$ 的比值为 $\frac{\sqrt{5}-1}{2}$ 时，扇面的形状较为美观，则此时扇形 $O C D$ 的半径与半圆 $O$ 的半径之比为
$\text{A.}$ $\frac{\sqrt{5}+1}{4}$
$\text{B.}$ $\frac{\sqrt{5}-1}{2}$
$\text{C.}$ $3-\sqrt{5}$
$\text{D.}$ $\sqrt{5}-2$
已知角 $\alpha$ 的顶点在坐标原点，始边与 $x$ 轴的非负半轴重合，终边上一点 $M$ 的坐标为 $\left(\sin \frac{3 \pi}{4}, \cos \frac{3 \pi}{4}\right)$ ，则角 $\alpha$ 的最小正角为 $(\quad)$
$\text{A.}$ $\frac{\pi}{4}$
$\text{B.}$ $\frac{3 \pi}{4}$
$\text{C.}$ $\frac{5 \pi}{4}$
$\text{D.}$ $\frac{7 \pi}{4}$
若角 $\alpha$ 的终边经过点 $P(1,-2)$ ，则 $\sin \alpha$ 的值为
$\text{A.}$ $\frac{2 \sqrt{5}}{5}$
$\text{B.}$ $\frac{\sqrt{5}}{5}$
$\text{C.}$ $-\frac{\sqrt{5}}{5}$
$\text{D.}$ $-\frac{2 \sqrt{5}}{5}$
已知角 $\theta$ 的终边经过点 $P\left(\frac{1}{2},-\frac{\sqrt{3}}{2}\right)$ ，则角 $\theta$ 可以为
$\text{A.}$ $\frac{5 \pi}{6}$
$\text{B.}$ $\frac{2 \pi}{3}$
$\text{C.}$ $\frac{11 \pi}{6}$
$\text{D.}$ $\frac{5 \pi}{3}$
若点 $\left(\sin \frac{5 \pi}{6}, \cos \frac{5 \pi}{6}\right)$ 在角 $\alpha$ 的终边上，则 $\sin \alpha$ 的值为
$\text{A.}$ $\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ $-\frac{\sqrt{3}}{2}$
已知角 $\alpha$ 的始边与 $x$ 轴非负半轴重合，终边上一点 $P(\sin 3, \cos 3)$ ，若 $0 \leq \alpha \leq 2 \pi$ ，则 $\alpha=$
$\text{A.}$ 3
$\text{B.}$ $\frac{\pi}{2}-3$
$\text{C.}$ $\frac{5 \pi}{2}-3$
$\text{D.}$ $3-\frac{\pi}{2}$
若角 $\alpha$ 满足 $\sin \alpha \cdot \cos \alpha < 0, \cos \alpha-\sin \alpha < 0$ ，则 $\alpha$ 在
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
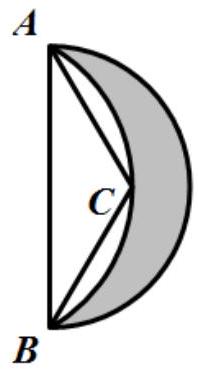
希波克拉底是古希腊医学家，他被西方尊为＂医学之父＂，除了医学，他也研究数学．特别是与＂月牙形＂有关的问题．如图所示．阴影部分的月牙形的边缘都是圆弧，两段圆弧分别是 VAB
$\text{A.}$ 的外接圆和以 $A B$ 为直径的圆的一部分，若 $\angle A C B=\frac{2 \pi}{3}, A C=B C=1$ ，则该月牙形的面积为（ ）
$\text{B.}$ $\frac{\sqrt{3}}{4}+\frac{\pi}{24}$
$\text{C.}$ $\frac{\sqrt{3}}{4}-\frac{\pi}{24}$
$\text{D.}$ $\frac{1}{4}+\frac{\pi}{24}$
$\text{E.}$ $\frac{1}{4}-\frac{\pi}{24}$
多选题 （共 1 题 ），每题有多个选项正确
下列结论中，正确的是（ ）
$\text{A.}$ $-\frac{7 \pi}{6}$ 是第三象限角
$\text{B.}$ 若圆心角为 $\frac{\pi}{3}$ 的扇形的弧长为 $\pi$ ，则该扇形的面积为 $\frac{3 \pi}{2}$
$\text{C.}$ 若角 $\alpha$ 的终边过点 $P(-3,4)$ ，则 $\cos \alpha=-\frac{3}{5}$
$\text{D.}$ 若角 $\alpha$ 为锐角，则角 $2 \alpha$ 为钝角
填空题 （共 7 题 ），请把答案直接填写在答题纸上
在平面直角坐标系中，角 $\alpha$ 的顶点在坐标原点，始边在 $x$ 轴的非负半轴，终边过点 $(-2$ ， $y)$ ，且 $\tan (\pi-\alpha)=2$ ，则 $\sin \alpha=$ $\qquad$。
终边在直线 $y=\sqrt{3} x$ 上的角的集合为 $\qquad$ ；
若角 $\theta$ 的终边与 $\frac{6 \pi}{7}$ 角的终边相同，则在 $[0,2 \pi)$ 内，终边与角 $\frac{\theta}{3}$ 的终边相同的角的个数为 $\qquad$ ；
已知在半径为 10 的圆 $O$ 中，弦 $A B$ 的长为 10 ．
（1）求弦 $A B$ 所对圆心角 $\alpha$ 的大小；
（2）求 $\alpha$ 所在的扇形弧长 $l$ 及弧所在弓形的面积 $S$ ．
已知角 $\alpha$ 的终边上一点 $P(-\sqrt{3}, m)(m \neq 0)$ ，且 $\sin \alpha=\frac{\sqrt{2} m}{4}$ ，求 $\cos \alpha, \tan \alpha$ 的值．
已知角 $\alpha$ 的终边过点 $P\left(-8 m,-6 \cos 60^{\circ}\right)$ ，且 $\cos \alpha=-\frac{4}{5}$ ，则 $m=$ $\qquad$ ．
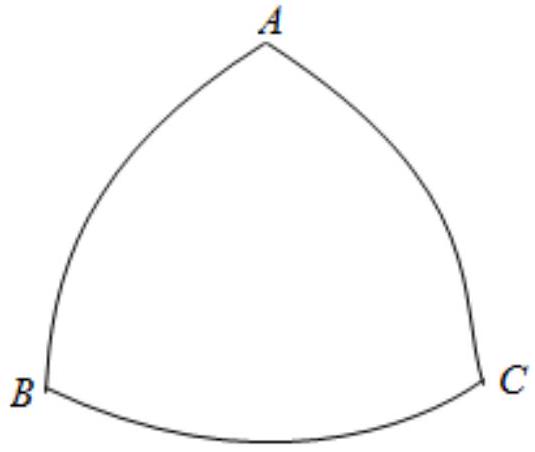
数学中处处存在着美，机械学家莱洛发现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形 $A B C$ ，再分别以点 $A 、 B 、 C$ 为圆心，线段 $A B$ 长为半径画圆弧，便得到莱洛三角（如图所示）．若莱洛三角形的周长为 $2 \pi$ ，则其面积是 $\qquad$ ．
