解答题 (共 19 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设随机变量 $X$ 的概率分布为
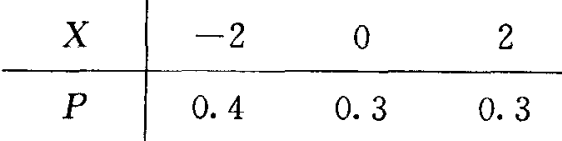
求 $E(3 X+5), D(2 X+3)$ .
据统计,一位 40 岁的健康者(体验未发现病症者),在五年之内仍然活着的概率为 $p(0 < p < 1), p$ 为已知,在五年内死亡的概率为 $1-p$ 。保险公司开办五年人寿保险,参加者需交保险费 $a$ 元( $a>0$ ,为已知)。若五年之内死亡,公司赔偿 $b$ 元 $(b>a)$ ,问 $b$ 的取值在什么范围内公司才可能获利?
假设一部机器在一天内发生故障的概率为 0.2 ,机器发生故障时全天停止工作。若一周 5 个工作日里无故障,可获利润 10 万元;发生一次故障仍可获利润 5 万元;发生二次故障可获利润 0 元;发生三次或三次以上故障就要亏损 2 万元.求一周内期望利润是多少?
某产品的次品率为 0.1 ,检验员每天检验 4 次.每次随机地取 10 件产品进行检验,如发现其中的次品数多于 1 ,就去调整设备.以 $X$表示一天中调整设备的次数,试求 $E X$ 和 $D X$(设诸产品是否为次品是相互独立的).
设袋中有 $m$ 只白球和 $n$ 只黑球,从中有放回地摸出 $s$ 只球,试求摸得白球只数的数学期望和方差。
将 $n$ 只球投人 $M$ 只盒子中去,每只球落入各个盒子是等可能的,求有球盒子数的数学期望.
设袋中有 2 个红球和 3 个绿球,$n$ 个人轮流摸球,每人摸出 2个球,然后将球放回袋中,让下一个人摸,求 $n$ 个人总共摸到红球数的数学期望和方差。
设事件 $A$ 在第 $i$ 次试验时发生的概率为 $p_i, i=1,2, \cdots, n$ ,且在各次试验中 $A$ 是否发生是相互独立的。求事件 $A$ 在 $n$ 次试验中发生次数的数学期望和方差.
一个碗中放有 10 个筹码,其中 8 个都标有 2,2 个都标有 5 .某人从此碗中随机地无放回地抽取 3 个筹码。若他获得的奖金等于所抽 3 个筹码的数字之和,求他平均获奖的数额。
假设公共汽车起点站于每小时的 10 分, 30 分和 50 分发车.某乘客不知发车的时间,在每小时内任一时刻到达车站是随机的,求乘客到车站等车时间的数学期望。
设由自动生产线加工的某种零件的内径 $X$(毫米)服从正态分布 $N(\mu, 1)$ ,内径小于 10 或大于 12 的为不合格品,余下的为合格品,销售每件合格品获利,销售不合格品亏损。已知销售利润 $T$(元)与销售零件内径有如下关系:
$$
T=\left\{\begin{array}{cc}
-1 & X < 10 \\
20 & 10 \leqslant X \leqslant 12 \\
-5 & X>12
\end{array}\right.
$$
问平均内径 $\mu$ 取何值时销售一个零件的平均利润最大?
一商店经销某种商品,每周进货量 $X$ 与顾客对该种商品的需求量 $Y$ 是相互独立的随机变量,且都服从均匀分布 $U[10,20]$ .商店每售出一单位商品可得到利润 1000 元;若需求量超过了进货量,商店可从其他商店调剂,这时每单位商品可获利润为 500 元。试计算此商店经销该种商品每周所得利润的期望值.
一汽车沿一街道行驶,需要通过三个均设有红绿信号灯的路口,每个信号灯为红或绿与其他信号灯为红或绿相互独立,且红绿两种信号显示的时间相等.以 $X$ 表示该汽车首次遇到红灯前已通过的路口的个数.求:
(1)$X$ 的概率分布;
(2)$E\left(\frac{1}{1+X}\right)$ .
设 $X$ 为 $n$ 次重复独立试验中事件 $A$ 出现的次数,且 $P(A)=$
$$
\begin{aligned}
& p, 0 < p < 1, \text { 令 } \\
& Y= \begin{cases}1 & \text { 当 } X \text { 为奇数时 } \\
0 & \text { 当 } X \text { 为偶数时 }\end{cases}
\end{aligned}
$$
求 $E Y$ .
设连续型随机变量 $X$ 的分布函数为
$$
F(x)=\left\{\begin{array}{cc}
0 & x < 0 \\
k x+b & 0 \leqslant x < \pi \\
1 & x \geqslant \pi
\end{array}\right.
$$
(1)试确定常数 $k, b$ 的值;
(2)求 $E X$ 和 $D X$ ;
(3)若 $Y=\sin X$ ,求 $E Y$ .
设随机变量 $X$ 的密度函数为
$$
p(x)=\frac{1}{\pi\left(1+x^2\right)} \quad-\infty < x < +\infty
$$
求 $E[\min \{|X|, 1\}]^2$ .
设二维随机向量 $(X, Y)$ 服从在区域 $D$ 上的二维均匀分布,其中区域 $D: 0 < x < 1,|y| < x$ .求关于 $X$ 的边际密度函数 $p_X(x)$ 和随机变量 $Z=2 X+1$ 的方差 $D Z$ .
在长为 $a$ 的线段上任取两点,求两点距离的数学期望和方差.
设随机变量 $X$ 和 $Y$ 相互独立且均服从 $N\left(0, \frac{1}{2}\right)$ ,求 $E|X-Y|$及 $D(|X-Y|)$ 。