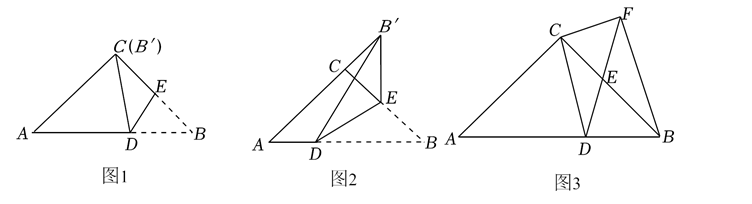
在 $\triangle A B C$ 中, $A C=B C=5, \tan B=\frac{3}{4}$, 点 $D 、$ 点 $E$ 分别是 $A B 、 B C$ 边上的动点.
(1) 连接 $D E$, 作 $\triangle B D E$ 关于 $D E$ 的对称图形 $\triangle B^{\prime} D E$.
(1) 如图 1, 当点 $B^{\prime}$ 恰好与点 $C$ 重合, 求 $D E$ 的长;
(2)如图 2, 当点 $B^{\prime}$ 落在 $A C$ 的延长线上, 且 $B^{\prime} E \perp A B$, 求 $B D$ 的长;
(2) 在点 $D 、 E$ 运动过程中, 满足 $C D^2=C E \cdot C B$, 过点 $C$ 作 $C F \perp C D$ 交射线 $D E$ 于点 $F$, 是否存在某个位置,
使得 $F D=F B$ ? 若存在, 求出此时 $A D$ 的长; 若不存在, 请说明理由.