一、单选题 （共 44 题，每小题 5 分，共 50 分，每题只有一个选项正确）
一个正多边形, 它的每一个外角都等于 $40^{\circ}$, 则该正多边形是 ( )
$\text{A.}$ 正六边形
$\text{B.}$ 正七边形
$\text{C.}$ 正八边形
$\text{D.}$ 正九边形
如图, $\triangle A B C \cong \triangle B A D$, 点 $A$ 和点 $B$, 点 $C$ 和点 $D$ 是对应点, 如果 $A B=6 \mathrm{~cm}, B D=5 \mathrm{~cm}, A D=4 \mathrm{~cm}$, 那么 $A C$ 的长是
$\text{A.}$ 4cm
$\text{B.}$ 5cm
$\text{C.}$ 6cm
$\text{D.}$ 无法确定
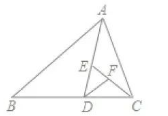
如图, $A D$ 是 $\triangle A B C$ 的中线, $C E$ 是 $\triangle A C D$ 的中线, $D F$ 是 $\triangle C D E$ 的中线, 如果 $\triangle D E F$ 的面积是 2 , 那么 $\triangle A B C$ 的面积为
$\text{A.}$ 12
$\text{B.}$ 14
$\text{C.}$ 16
$\text{D.}$ 18
如图, 在锐角 $\triangle A B C$ 中, $C D, B E$ 分别是 $A B, A C$ 边上的高, 且 $C D, B E$ 相交于一点 $P$, 若 $\angle A=50^{\circ}$, 则 $\angle B P C=$
$\text{A.}$ $150^{\circ}$
$\text{B.}$ $130^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $100^{\circ}$
已知 $A D$ 是 $\triangle A B C$ 的一条中线, $A B=9, A C=7$, 则 $A D$ 的取值范围是（ )
$\text{A.}$ $7 < A D < 9$
$\text{B.}$ $2 < A D < 16$
$\text{C.}$ $1 < A D < 8$
$\text{D.}$ $7 < A D < 8$
如图, $\angle A O B$ 是一钢架, $\angle A O B=15^{\circ}$, 为使钢架更加牢固, 需在其内部添加一些钢管 $E F 、 F G$ 、 $G H \cdots$ 添的钢管长度都与 $O E$ 相等, 则最多能添加这样的钢管（）根.
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 无数
如图, 已知线段 $A B=20$ 米, $M A \perp A B$ 于点 $A, M A=6$ 米, 射线 $B D \perp A B$ 于, $P$ 点从 $B$ 点向 $A$ 运动, 每 秒走 1 米, $Q$ 点从 $B$ 点向 $D$ 运动, 每秒走 3 米, $P 、 Q$ 同时从 $B$ 出发, 则出发 $x$ 秒后, 在线段 $M A$ 上有一点 $C$, 使 $\triangle C A P$ 与 $\triangle P B Q$ 全等, 则 $x$ 的值为（）
$\text{A.}$ 5
$\text{B.}$ 5或10
$\text{C.}$ 10
$\text{D.}$ 6或10
如图, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}$, 将 Rt $\triangle A B C$ 绕点 $C$ 按 顺时针方向旋转一定角度得到 Rt $\triangle D E C$, 点 $D$ 恰好落在边 $A B$ 上. 若 $\angle B=20^{\circ}$, 则 $\angle B C E$ 的度数为
$\text{A.}$ $20^{\circ}$
$\text{B.}$ $40^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $80^{\circ}$
三角形两边的长是 4 和 9 , 第三边满足方程 $x^2-24 x+140=0$, 则三角形周长为 ( )
$\text{A.}$ 27
$\text{B.}$ 23
$\text{C.}$ 23 或 27
$\text{D.}$ 以上都不对
如图所示的衣架可以近似看成一个等腰三角形 $A B C$, 其中 $A B=A C, \angle A B C=27^{\circ}, B C=44 \mathrm{~cm}$, 则高 $A D$ 约为
(参考数据: $\sin 27^{\circ} \approx 0.45, \cos 27^{\circ} \approx 0.89, \tan 27^{\circ} \approx 0.51$ )
$\text{A.}$ $9.90 \mathrm{~cm}$
$\text{B.}$ $11.22 \mathrm{~cm}$
$\text{C.}$ $19.58 \mathrm{~cm}$
$\text{D.}$ $22.44 \mathrm{~cm}$
下列各组数中, 是勾股数的是
$\text{A.}$ $1,1, \sqrt{2}$
$\text{B.}$ $9,12,15$
$\text{C.}$ $4,5,6$
$\text{D.}$ $1.5,2.5,2$
本学期, 我们学习了用赵爽弦图证明勾股定理. 在如图所示的赵爽弦图中, 在 $D H$ 上取点 $M$ 使得 $D M=G H$, 连接 $A M 、 C M$. 若正方形 $E F G H$ 的面积为 6, 则 $\triangle A D M$ 与 $\triangle C D M$ 的面积之差为
$\text{A.}$ 3
$\text{B.}$ 2
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 不确定
如图, 在 $R f \mathrm{~V} A B C$ 中, $D$ 为斜边 $A C$ 的中点, $E$ 为 $B D$ 上一点, $F$ 为 $C E$ 中点. 若 $A E=A D, D F=2$, 则 $B D$ 的长为
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ 3
$\text{C.}$ $2 \sqrt{3}$
$\text{D.}$ 4
将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形$ABCD$内，其中矩形纸片和正方形纸片的周长相等．若知道图中阴影部分的面积，则一定能求出
$\text{A.}$ 正方形纸片的面积
$\text{B.}$ 四边形EFGH的面积
$\text{C.}$ VBEF的面积
$\text{D.}$ $\triangle AEH$的面积
如图, $\triangle A B D$ 是等边三角形, $\triangle C B D$ 是等腰三角形, 且 $B C=D C$, 点 $E$ 是边 $A D$ 上 的一点, 满足 $C E / / A B$, 如果 $A B=8, C E=6$, 那么 $B C$ 的长是
$\text{A.}$ 6
$\text{B.}$ $2 \sqrt{7}$
$\text{C.}$ $ \sqrt{43}$
$\text{D.}$ $3 \sqrt{3}$
某学校安装红外线体温检测仪 (如图 1), 其红外线探测点 $O$ 可以在垂直于地面的支杆 $O P$ 上自由调节 (如图 2). 已知最大探测角 $\angle O B C=67^{\circ}$, 最小探测角 $\angle O A C=37^{\circ}$. 测温区域 $A B$ 的长度为 2 米, 则该设备的安装高度 $O C$ 应调整为 $(\quad)$ 米. (精确到 $0.1$ 米.
参考数据: $\sin 67^{\circ} \approx \frac{12}{13}, \cos 67^{\circ} \approx \frac{5}{13}, \tan 67^{\circ} \approx \frac{12}{5}, \sin 37^{\circ} \approx \frac{3}{5}, \cos 37^{\circ} \approx \frac{4}{5}, \tan 37^{\circ} \approx \frac{3}{4}$ )
$\text{A.}$ $2.4$
$\text{B.}$ $2.2$
$\text{C.}$ $3.0$
$\text{D.}$ $2.7$
如图 3, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, D$ 是 $A B$ 的中点, 延长 $C B$ 至点 $E$, 使 $B E=B C$,
连接 $D E, F$ 为 $D E$ 中点, 连接 $B F$. 若 $A C=16, B C=12$, 则 $B F$ 的长为
$\text{A.}$ 5
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 8
如图 4, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, \angle A=30^{\circ}, B C=2$, 将 $\triangle A B C$ 绕点 $C$ 顺时针旋转得到 $\triangle A^{\prime} B^{\prime} C$, 其中点 $A^{\prime}$ 与点 $A$ 是对应点, 点 $B^{\prime}$ 与点 $B$ 是对应点.若点 $B^{\prime}$ 恰好落在 $A B$ 边上, 则点 $A$ 到直线 $A^{\prime} C$ 的 距离等于
$\text{A.}$ $3 \sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $3$
$\text{D.}$ $2$
如图, 在 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, C D$ 是 $\triangle A B C$ 的中线, $A C=8, A B=12$, 则 $C D$ 的长等于
$\text{A.}$ 5
$\text{B.}$ 4
$\text{C.}$ 8
$\text{D.}$ 6
如图, 在菱形 $A B C D$ 中摆放了一副三角板. 等腰直角三角板 $D E F$ 的一条直角边 $D E$ 在菱形边 $A D$ 上, 直角顶点 $E$ 为 $A D$ 的中点, 含 $30^{\circ}$ 角的直角三角板的斜边 $G B$ 在菱形 $A B C D$ 的边 $A B$ 上. $\angle C D F$ 的度数等于
$\text{A.}$ $55^{\circ}$
$\text{B.}$ $65^{\circ}$
$\text{C.}$ $75^{\circ}$
$\text{D.}$ $85^{\circ}$
如图，数轴上$A,B$两点到原点的距离是三角形两边的长，则该三角形第三边长可能是
$\text{A.}$ -5
$\text{B.}$ 4
$\text{C.}$ 7
$\text{D.}$ 8
如图, 在菱形纸片 $\mathrm{ABCD}$ 中, $\mathrm{E}$ 是 $\mathrm{BC}$ 边上一点, 将 $\triangle$ $\mathrm{ABE}$ 沿直线 $\mathrm{AE}$ 翻折, 使点 $\mathrm{B}$ 落在 $\mathrm{B}^{\prime}$ 上, 连接 $\mathrm{DB}$ '. 已知 $\angle \mathrm{C}=$ $120^{\circ}, \angle \mathrm{BAE}=50^{\circ}$, 则 $\angle \mathrm{AB}$ 'D 的度数为
$\text{A.}$ $50^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $80^{\circ}$
$\text{D.}$ $90^{\circ}$
如图, 五角星绕着它的旋转中心旋转, 使得 $\triangle A B C$ 与 $\triangle D E F$ 重合,那么旋转角的度数至少为.
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $120^{\circ}$
$\text{C.}$ $72^{\circ}$
$\text{D.}$ $144^{\circ}$
如图, 在 $\triangle A B C$ 中, $D 、 E$ 分别为线段 $B C 、 B A$ 的中点, 设 $\triangle A B C$ 的面积为 $S_1$, $\Delta \mathrm{EBD}$
的面积为 $S_2$. 则 $\frac{s_1}{s_2}=$
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{7}{8}$
如图, $O B$ 平分 $\angle A O C, D 、 E 、 F$ 分别是射线 $O A$ 、射线 $O B 、$ 射线 $O C$ 上的点, $D 、 E 、 F$ 与 $O$ 点都不重合, 连接 $E D 、 E F$ 若添加下列条件中的某一个.就能使 $\triangle D O E$ $\cong \triangle \mathrm{FOE}$, 你认为要添加的那个条件是
$\text{A.}$ $\mathrm{OD}=\mathrm{OE}$
$\text{B.}$ $\mathrm{OE}=\mathrm{OF}$
$\text{C.}$ $\angle \mathrm{ODE}=\angle \mathrm{OED}$
$\text{D.}$ $\angle \mathrm{ODE}=\angle \mathrm{OFE}$
将一副直角三角板按如图所示的位置摆放, 若 $D E / / A C$, 则图中 $\angle 1$ 的 度数是
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $75^{\circ}$
$\text{C.}$ $90^{\circ}$
$\text{D.}$ $105^{\circ}$
如图, 一棵大树被台风拦腰刮断, 树根 $A$ 到刮断点 $P$ 的长度是 $4 m$, 折断部分 $P B$ 与地面成 $40^{\circ}$ 的夹角, 那 么原来树的长度是
$\text{A.}$ $4+\frac{4}{\cos 40^{\circ}}$ 米
$\text{B.}$ $4+\frac{4}{\sin 40^{\circ}}$ 米
$\text{C.}$ $4+4 \sin 40^{\circ}$ 米
$\text{D.}$ $4+4 \cot 40^{\circ}$ 米
如图, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, A C=6, B C=8$, 将 Rt $\triangle A B C$ 绕点 $B$ 顺时针旋转 $90^{\circ}$ 得到 $R t \triangle A^{\prime} B^{\prime} C^{\prime}$. 在此旋转过程中 $R t \triangle A B C$ 所扫过的面积为
$\text{A.}$ $25 \pi+24$
$\text{B.}$ $5 \pi+24$
$\text{C.}$ $25 \pi$
$\text{D.}$ $5 \pi$
如图, $\triangle A B C$ 与 $\triangle D E F$ 位似, 点 $O$ 为位似中心, 相似比为 $2: 3$. 若 $\triangle A B C$ 的周长为 4 , 则 $\triangle D E F$ 的周长是
$\text{A.}$ 4
$\text{B.}$ 6
$\text{C.}$ 9
$\text{D.}$ 10
如图, 在 $\triangle A B C$ 中, $\angle C D E=64^{\circ}, \angle A=28^{\circ}, D E$ 垂直平分 $B C$, 则 $\angle A B D=$
$\text{A.}$ $100^{\circ}$
$\text{B.}$ $128^{\circ}$
$\text{C.}$ $108^{\circ}$
$\text{D.}$ $98^{\circ}$
如图, $\triangle A B C$ 的外角平分线 $B D, C E$ 相交于点 $P$. 若点 $P$ 到 $A C$ 的距离为 3 , 则点 $P$ 到 $A B$ 的距离为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
如图, 在 $\triangle A B C$ 中, $\angle B=30^{\circ}, \angle C=45^{\circ}, A D$ 平分 $\angle B A C$ 交 $B C$ 于 点 $D, D E \perp A B$, 垂足为 $E$. 若 $D E=1$, 则 $B C$ 的长为
$\text{A.}$ $2+\sqrt{2}$
$\text{B.}$ $\sqrt{2}+\sqrt{3}$
$\text{C.}$ $2+\sqrt{3}$
$\text{D.}$ $3$
已知直角三角形两条直角边的边长之和为 $\sqrt{6}$, 斜边长为 2 , 则这个三角形的面积是
$\text{A.}$ $0.25$
$\text{B.}$ $0.5$
$\text{C.}$ $1$
$\text{D.}$ $2 \sqrt{3}$
到三角形三个顶点距离相等的是
$\text{A.}$ 三条中线交点
$\text{B.}$ 三条高的交点
$\text{C.}$ 三条角平分线的交点
$\text{D.}$ 三条中垂线的交点
如图,在距某居民楼 $A B$ 楼底 $B$ 点左侧水平距离 $60 \mathrm{~m}$ 的 $C$ 点处有一个山坡, 山坡 $\mathrm{CD}$ 的坡度 (或坡比) $i=1: 0.75$, 山坡坡底 $C$ 点到坡顶 $D$ 点的距离 $C D=45 \mathrm{~m}$, 在坡顶 $D$ 点处测得居民楼楼顶 $A$ 点的仰角为 $28^{\circ}$, 居民楼 $A B$ 与山坡 $C D$ 的剖面在同一平面内, 则居民楼 $A B$ 的高度约为
(参考数据: $\sin 28^{\circ} \approx 0.47, \cos 28^{\circ} \approx 0.88, \tan 28^{\circ} \approx 0.53$ )
$\text{A.}$ $76.9 \mathrm{~m}$
$\text{B.}$ $82.1 \mathrm{~m}$
$\text{C.}$ $94.8 \mathrm{~m}$
$\text{D.}$ $112.6 \mathrm{~m}$
如图, 在已知的 $\triangle A B C$ 中, 按以下步骤作图：(1)分 别以 $B 、 C$ 为圆心, 以大于 $\frac{1}{2} B C$ 的长为半径作弧, 两弧相交于 点 $M 、 N$; (2)作直线 $M N$ 交 $A B$ 于点 $D$, 连接 $C D$, 若 $C D=A D$, $\angle B=20^{\circ}$, 则下列结论中错误的是
$\text{A.}$ $\angle C A D=40^{\circ}$
$\text{B.}$ $\angle A C D=70^{\circ}$
$\text{C.}$ 点 $D$ 为 $\triangle A B C$ 的外心
$\text{D.}$ $\angle A C B=90^{\circ}$
如图, 在平面直角坐标系中, 有点 $A(6,3), B(6,0)$, 以原点 $O$ 为位似中心, 在第一象 限内将线段 $A B$ 缩小后得到线段 $C D$, 点 $A$ 的对应点为点 $C$. 若 $\triangle O C D$ 与 $\triangle O A B$ 的相似比为 $\frac{1}{3}$, 则点 $C$ 的坐标为
$\text{A.}$ $(2,1)$.
$\text{B.}$ $(2,0)$.
$\text{C.}$ $(3,1)$.
$\text{D.}$ $(3,0)$.
如图, 在 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, C D$ 是斜边 $A B$ 的中线, 过点 $D$ 作 $D E \perp A C$, 垂足为点 $E$. 若 $\sin A=\frac{1}{3}, A B=6$, 则 $\triangle C D E$ 的周长为
$\text{A.}$ $4+2 \sqrt{2}$.
$\text{B.}$ $4+4 \sqrt{2}$.
$\text{C.}$ $6+2 \sqrt{2}$.
$\text{D.}$ $6+4 \sqrt{2}$.
某品牌 20 寸的行李箱拉杆拉开后放置如图所示, 经测量该行李 箱从轮子底部到箱子上沿的高度 $A B$ 与从轮子底部到拉杆顶部的 高度 $C D$ 之比是黄金比 (约等于 0.618 ). 已知 $C D=80 \mathrm{~cm}$, 则 $A B$ 约是
$\text{A.}$ $30 \mathrm{~cm}$
$\text{B.}$ $49 \mathrm{~cm}$
$\text{C.}$ $55 \mathrm{~cm}$
$\text{D.}$ $129 \mathrm{~cm}$