单选题 (共 5 题 ),每题只有一个选项正确
双曲线 $\frac{x^2 y^2}{4 \frac{5}{5}}=1$ 的焦点坐标为
$\text{A.}$ $(0, \pm 1)$
$\text{B.}$ $( \pm 1,0)$
$\text{C.}$ $(0, \pm 3)$
$\text{D.}$ $( \pm 3,0)$
已知命题 $p: \forall n \in N^*, n^2>\frac{1}{2} n-1$, 则命题 $p$ 的否定命题 为 ( )
$\text{A.}$ $\exists {n} \in {N}^*, {n}^2 \leq \frac{1}{2} {n}-1$
$\text{B.}$ $\forall {n} \in {N}^*, {n}^2 < \frac{1}{2} {n}-1$
$\text{C.}$ $\forall {n} \in {N}^*, {n}^2 \leq \frac{1}{2^n-1}$
$\text{D.}$ $\exists n \in N^*, n^2 < \frac{1}{2} {n}-1$
经过点 $(2,4)$ 的抛物线的标准方程为
$\text{A.}$ $y^2=8 x$
$\text{B.}$ $x^2=y$
$\text{C.}$ $y^2=8 x$ 或 $x^2=y$
$\text{D.}$ 无法确定
已知空间向量 $\vec{m}=(1,3, x), \vec{n}=\left(x^2,-1,2\right)$, 则 " $x=1$ " 是 " $\vec{m} \perp \vec{n}$ " 的 ( )
$\text{A.}$ 必要不充分条件
$\text{B.}$ 充分不必要条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
如图, 在三棱锥 $\mathrm{C}-\mathrm{OAB}$ 中, $\mathrm{OA} \perp \mathrm{OB}, \mathrm{OC} \perp$ 平面 $\mathrm{OAB}, \mathrm{OA}=6, \mathrm{OB}=\mathrm{OC}=8, \mathrm{CE}=\frac{1}{4} \mathrm{CB}$,
$D, F$ 分别为 $A B, B C$ 的中点, 则异面直线 $D F$ 与 $O E$ 所成角的余弦值为
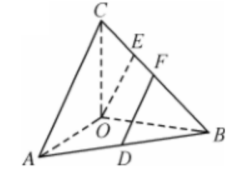
$\text{A.}$ $\frac{\sqrt{10}}{10}$
$\text{B.}$ $\frac{6 \sqrt{10}}{25}$
$\text{C.}$ $\frac{\sqrt{30}}{30}$
$\text{D.}$ $\frac{\sqrt{30}}{20}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
已知曲线 $l_1: x-y+3=0$, 直线 $l_2: x=-3$, 则抛物线 $x=\frac{1}{8} y^2$ 上一个动点 $P$ 到直线 $l_1$ 的距离与它到直线 $l_2$ 的距离之和的最小值为
若双曲线 $\frac{x^2}{a^2-y^2}=1$ 的一个焦点到一条渐近线的距离为 2 a , 则双曲线的离心率为
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知抛物线 ${x}^2=2 {py}({p}>0)$, 焦点到准线的距离为 4 .
(1) 求抛物线的方程;
(2) 若抛物线上存在两点关于直线 $y=2 x+m$ 对称, 且两点的横坐标之积为 2 , 求 $m$ 的值.
如图, 已知四棱锥 $ {P}- {ABCD}$ 的底面是正方形, $ {PA} \perp$ 平面 $ {ABCD}, {PA}= {AD}=2$, 点 $ {E}, {F}, {G}$ 分别为 $A B, A D, P C$ 的中点.
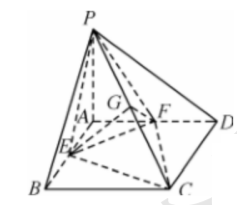
(1) 求证: ${PC} \perp$ 平面 EFG ;
(2) 求二面角E-PC-F的余弦值.