单选题 (共 1 题 ),每题只有一个选项正确
若图中的直线 $l_1, l_2, l_3$ 的斜率分别为 $k_1, k_2, k_3$, 则
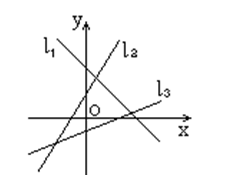
$\text{A.}$ $k_1 < k_2 < k_3$
$\text{B.}$ $k_3 < k_1 < k_2$
$\text{C.}$ $k_3 < k_2 < k_1$
$\text{D.}$ $k_1 < k_3 < k_2$
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在复平面上, 一个正方形的四个顶点按照逆时针方向依次为 $Z_1, Z_2, Z_3, O$ (其中 0 是原点), 已知 $Z_2$ 对应复数 $Z_2=1+\sqrt{3} i$. 求 $Z_1$ 和 $Z_3$ 对应的复数.
求 $\sin ^2 20^{\circ}+\cos ^2 50^{\circ}+\sin 20^{\circ} \cos 50^{\circ}$ 的值.
设 $\left\{a_n\right\}$ 是由正数组成的等比数列, $S_n$ 是其前 $n$ 项和.
(1) 证明 $\frac{\lg S_n+\lg S_{n+2}}{2} < \lg S_{n+1}$ ;
(2) 是否存在常数 $c>0$, 使得 $\frac{\lg \left(S_n-c\right)+\lg \left(S_{n+2}-c\right)}{2}=\lg \left(S_{n+1}-c\right)$ 成立? 并证明你的结论.
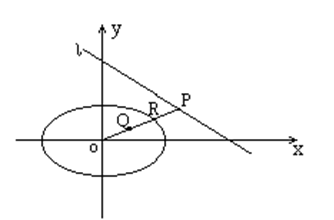
已 知椭圆 $\frac{x^2}{24}+\frac{y^2}{16}=1$, 直线 $l: \frac{x}{12}+\frac{y}{8}=1 . P$ 是 1 上点, 射线 $O P$ 交椭圆于点 $R$, 又点 $Q$ 在 $O P$ 上且满足 $|O Q| \cdot|O P|=|O R|$, 当点 $P$ 在 1 上移动时, 求点 $Q$ 的轨迹方程, 并说明轨迹是什么曲线。