单选题 (共 5 题 ),每题只有一个选项正确
若 $y=x^2+a x+b$ 和 $2 y=-1+x y^3$ 在 $(1,-1)$ 点相切,其中 $a, b$ 是常数,则
$\text{A.}$ $a=0, b=-2$
$\text{B.}$ $a=1, b=-3$
$\text{C.}$ $a=-3, b=1$
$\text{D.}$ $a=-1, b=-1$
设函数 $f(x)=\left\{\begin{array}{cc}x^2 & 0 \leq x \leq 1 \\ 2-x & 1 < x \leq 2\end{array}\right.$ ,记$F(x)=\int_0^x f(t) \mathrm{d} t, 0 \leq x \leq 2$, 则
$\text{A.}$ $F(x)=\left\{\begin{array}{cl}\frac{x^3}{3}, & 0 \leq x \leq 1 \\ \frac{1}{3}+2 x-\frac{x^2}{2}, & 1 < x \leq 2\end{array}\right.$
$\text{B.}$ $F(x)=\left\{\begin{array}{cc}\frac{x^3}{3}, & 0 \leq x \leq 1 \\ -\frac{7}{6}+2 x-\frac{x^2}{2}, 1 < x \leq 2\end{array}\right.$
$\text{C.}$ $F(x)=\left\{\begin{array}{cr}\frac{x^3}{3}, & 0 \leq x \leq 1 \\ \frac{x^3}{3}+2 x-\frac{x^2}{2}, 1 < x \leq 2\end{array}\right.$
$\text{D.}$ $F(x)=\left\{\begin{array}{c}\frac{x^3}{3}, \quad 0 \leq x \leq 1 \\ 2 x-\frac{x^2}{2}, 1 < x \leq 2\end{array}\right.$
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内有定义, $x_0 \neq 0$ 是函数 $f(x)$ 的极大值点,则
$\text{A.}$ $x_0$ 必是 $f(x)$ 的驻点
$\text{B.}$ $-x_0$ 必是 $-f(-x)$ 的极小值点
$\text{C.}$ $-x_0$ 必是 $-f(x)$ 的极小值点
$\text{D.}$ 对一切 $x$ ,都有 $f(x) \leq f\left(x_0\right)$
曲线 $y=\frac{1+e^{-x^2}}{1-e^{-x^2}}$
$\text{A.}$ 没有渐近线
$\text{B.}$ 仅有水平渐近线
$\text{C.}$ 仅有铅直渐近线
$\text{D.}$ 既有水平渐近线又有铅直渐近线
如图, $x$ 轴上有一线密度为常数 $\mu$ ,长度为 $l$ 的细杆,若质量为 $m$ 的质点到杆右端的距离为 $a$ ,已知引力系数为 $k$ ,则质点和细杆之间引力的大小为

$\text{A.}$ $\int_{-l}^0 \frac{k m \mu \mathrm{d} x}{(a-x)^2}$
$\text{B.}$ $\int_0^l \frac{k m \mu \mathrm{d} x}{(a-x)^2}$
$\text{C.}$ $2 \int_{-\frac{l}{2}}^0 \frac{k m \mu \mathrm{d} x}{(a+x)^2}$
$\text{D.}$ $2 \int_0^{\frac{l}{2}} \frac{k m \mu \mathrm{d} x}{(a+x)^2}$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
设 $y=\ln \left(1+3^{-x}\right)$, 则 $\mathrm{d} y=$
$\int_1^{+\infty} \frac{\ln x}{x^2} \mathrm{~d} x=$
质点以速度 $t \sin \left(t^2\right)$ 米秒作直线运动,则从时刻 $t_1=\sqrt{\frac{\pi}{2}}$到 $t_2=\sqrt{\pi}$ 秒内质点所经过的路程等于米.
$\lim _{x \rightarrow 0^{+}} \frac{1-e^{\frac{1}{x}}}{x+e^{\frac{1}{x}}}=$
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $\left\{\begin{array}{l}x=t \cos t \\ y=t \sin t\end{array}\right.$ ,求 $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}$
计算 $\int_1^4 \frac{\mathrm{d} x}{x(1+\sqrt{x})}$
求 $\lim _{x \rightarrow 0} \frac{x-\sin x}{x^2\left(e^x-1\right)}$.
求 $\int x \sin ^2 x \mathrm{~d} x$.
求微分方程 $x y^{\prime}+y=x e^x$ 满足 $y(1)=1$ 的特解.
利用导数证明: 当 $x>1$ 时,有不等式 $\frac{\ln (1+x)}{\ln x}>\frac{x}{1+x}$成立.
求微分方程 $y^{\prime \prime}+y=x+\cos x$ 的通解.
曲线 $y=(x-1)(x-2)$ 和 $x$ 轴围成一平面图形、求此平面图形绕 $y$ 轴旋转一周所成的旋转体的体积.
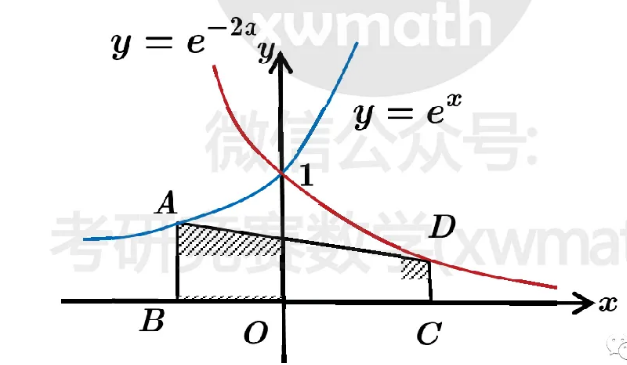
如图, $A$ 和 $D$ 分别是曲线 $y=e^x$ 和 $y=e^{-2 x}$ 上的点, $A B$ 和 $D C$ 均垂直 $x$ 轴,且
$$
|A B|:|D C|=2: 1,|A B| < 1,
$$
求点 $B$ 和 $C$ 的横坐标,使梯形 $A B C D$ 的面积最大.
设 $f(x)$ 在 $(-\infty,+\infty)$ 内满足
$$
f(x)=f(x-\pi)+\sin x .
$$
且 $f(x)=x, x \in[0, \pi)$ ,计算 $I=\int_\pi^{3 \pi} f(x) \mathrm{d} x$.