单选题 (共 6 题 ),每题只有一个选项正确
已知 $a=3^{55}, b=4^{44}, \mathrm{c}=5^{33}$, 则有
$\text{A.}$ $a < b < c$
$\text{B.}$ $c < b < a$
$\text{C.}$ $c < a < b$
$\text{D.}$ $a < c < b$
方程组 $\left\{\begin{array}{l}x y+y z=63 \\ x z-y z=23\end{array}\right.$ 的正整数解的组数是
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
如果方程 $(x-1)\left(x^2-2 x-m\right)=0$ 的三根可以作为一个三角形的三边之长, 那么实数 $m$ 的取值范围是
$\text{A.}$ $0 \leq \mathrm{m} \leq 1$
$\text{B.}$ $m \geq \frac{3}{4}$
$\text{C.}$ $\frac{3}{4} < \mathrm{m} \leq 1$
$\text{D.}$ $\frac{3}{4} \leq m \leq 1$
如果边长顺次为 $25 、 39 、 52$ 与 60 的四边形内接于一圆, 那么此圆的周长为
$\text{A.}$ $62 \pi$
$\text{B.}$ $63 \pi$
$\text{C.}$ $64 \pi$
$\text{D.}$ $65 \pi$
设 $A B$ 是 $\odot O$ 的一条弦, $C D$ 是 $\odot O$ 的直径, 且与弦 $A B$ 相交, 记M $=\mid S _{\triangle C A B}$ $-S_{\triangle D A B} \mid, N=2 S_{\triangle O A B}$, 则
$\text{A.}$ $\mathrm{M}>\mathrm{N}$
$\text{B.}$ $\mathrm{M}=\mathrm{N}$
$\text{C.}$ $\mathrm{M} < \mathrm{N}$
$\text{D.}$ $M、N$的大小关系不确定
设实数 $a 、 b$ 满足不等式 ||$a|-(a+b)| < |a-| a+b||$, 则
$\text{A.}$ $a>0$ 且 $b>0$
$\text{B.}$ $a < 0$ 且 $b>0$
$\text{C.}$ $a>0$ 且 $b < 0$
$\text{D.}$ $a < 0$ 且 $b < 0$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
在 $1^2, 2^2, 3^{2 \cdots}, 95^2$ 这 95 个数中, 十位数字为奇数的数共有
已知 $a$ 是方程 $x^2+x-\frac{1}{4}=0$ 的根, 则 $\frac{a^3-1}{a^5+a^4-a^3-a^2}$ 的值等于
设 $x$ 为正实数, 则函数 $\mathrm{y}=\mathrm{x}^2-\mathrm{x}+\frac{1}{\mathrm{x}}$ 的最小值是
以线段 $A B$ 为直径作一个半圆, 圆心为 $O, C$ 是半圆周上的点, 且 $O C^2=A C \cdot B C$,则 $\angle C A B=$
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
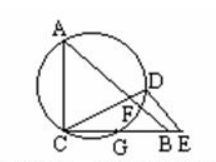
已知 $\angle \mathrm{ACE}=\angle \mathrm{CDE}=90^{\circ}$, 点 $\mathrm{B}$ 在 $\mathrm{CE}$ 上, $\mathrm{CA}=\mathrm{CB}=\mathrm{CD}$, 经 $\mathrm{A} 、 \mathrm{C} 、 \mathrm{D}$三点的圆交 $\mathrm{AB}$ 于 $\mathrm{F}$ (如图) 求证 $\mathrm{F}$ 为 $\triangle \mathrm{CDE}$ 的内心。
在坐标平面上, 纵坐标与横坐标都是整数的点称为整点, 试在二次函数 $y=\frac{x^2}{10}-\frac{x}{10}+\frac{9}{5}$ 的图象上找出满足 $y < |x|$ 的所有整点 $(x, y)$, 并说明理由
试证:每个大于 6 的自然数 $\mathrm{n}$, 都可以表示为两个大于 1 且互质的自然数之和。