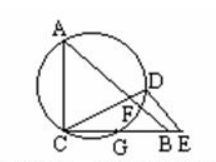
已知 $\angle \mathrm{ACE}=\angle \mathrm{CDE}=90^{\circ}$, 点 $\mathrm{B}$ 在 $\mathrm{CE}$ 上, $\mathrm{CA}=\mathrm{CB}=\mathrm{CD}$, 经 $\mathrm{A} 、 \mathrm{C} 、 \mathrm{D}$三点的圆交 $\mathrm{AB}$ 于 $\mathrm{F}$ (如图) 求证 $\mathrm{F}$ 为 $\triangle \mathrm{CDE}$ 的内心。