解答题 (共 14 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$\triangle A B C$ 的内角 $A 、 B 、 C$ 的对边分别为 $a 、 b 、 c$, 设 $(\sin B-\sin C)^2=\sin ^2 A-\sin B \sin C$.
(1)求 $A$.
(2) 若 $\sqrt{2} a+b=2 c$, 求 $\sin C$.
在 $\triangle A B C$ 中, $\sin 2 C=\sqrt{3} \sin C$.
(1) 求 $\angle C$.
(2)若 $b=6$, 且 $\triangle A B C$ 的面积为 $6 \sqrt{3}$, 求 $\triangle A B C$ 的周长.
在 $\triangle A B C$ 中, 内角 $A 、 B 、 C$ 所对应的边分别为 $a 、 b 、 c_3$ 且 $c=2 b_2 2 \sin A=3 \sin 2 C$.
(1)求 $\sin C$,
(2)若 $\triangle A B C$ 的面积为 $\frac{3 \sqrt{7}}{2}$, 求 $A B$ 边上的中线 $C D$ 的长。
求 $\tan 20^{\circ}+4 \sin 20^{\circ}$ 的值.
若 $\cos \alpha+\cos ^2 \alpha=1$, 求 $\sin ^2 \alpha+\sin ^6 \alpha$ 的值.
已知 $x \in\left(0, \frac{\pi}{2}\right)$, 且 $\cos ^2 x+\cos ^2 2 x+\cos ^2 3 x=1$, 求 $x$ 的值.
求 $\cos \frac{\pi}{7}+\cos \frac{3 \pi}{7}+\cos \frac{5 \pi}{7}$ 的值.
求 $\sin \left(\alpha+75^{\circ}\right)+\cos \left(\alpha+45^{\circ}\right)-\sqrt{3} \cos \left(\alpha+15^{\circ}\right)$ 的值.
若 $\cos ^3 x=\sin ^3 x+1$, 试求 $\sin x$ 的值.
已知 $\triangle A B C$ 中, $\sin A=\frac{5}{13}, \cos B=\frac{4}{5}$, 求 $\cos C$.
已知 $\sin \alpha+\sin \beta+\sin \gamma=0$, $\cos \alpha+\cos \beta+\cos \gamma=0$, 求 $\cos (\alpha-\beta)$ 的值.
已知 $\sin \alpha+\cos \alpha=\frac{1-\sqrt{3}}{2}$, 且 $\alpha$ 为第二象限角, 则 $\sin \alpha=$
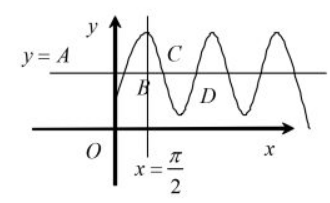
已知函数 $f(x)=A \sin x+1(A>1)$ 的图象与直线 $y=A$ 在 $x$ 轴右侧的与 $x$ 轴距离最近的相邻三个交点的横坐标成等比数列, 求实数 $A$ 的值.
求证 $\frac{2(\cos \alpha-\sin \alpha)}{1+\sin \alpha+\cos \alpha}=\frac{\cos \alpha}{1+\sin \alpha}-\frac{\sin \alpha}{1+\cos \alpha}$.