单选题 (共 10 题 ),每题只有一个选项正确
一定量的理想气体㧒于某一容器中, 温度为 $T$, 气体分子的质量为 $m$. 根据理想气体的分子模型和统计假设, 分子速 度在 $x$ 方向的分量平方的平均值
$\text{A.}$ $\overline{v_x^2}=\sqrt{\frac{3 k T}{m}}$
$\text{B.}$ $\overline{v_x^2}=\frac{1}{3} \sqrt{\frac{3 k T}{m}}$
$\text{C.}$ $\overline{\nu_x^2}=3 k T / m$
$\text{D.}$ $\overline{\nu_x^2}=k T / m$
三个容器 $A 、 B 、 C$ 中装有同种理想气体,其分子数密度 $n$ 相同,而方均根速率之比为 $\left(\overline{v_A^2}\right)^{1 / 2}:\left(\overline{v_B^2}\right)^{1 / 2}:\left(\overline{v_C^2}\right)^{1 / 2}=$ $1: 2: 4$, 则其压强之比 $p_A: p_B: p_C$ 为
$\text{A.}$ $1: 2: 4$
$\text{B.}$ $1: 4: 8$
$\text{C.}$ $1: 4: 16$
$\text{D.}$ $4: 2: 1$
已知氢气与氧气的温度相同,请判断下列说法哪个正确
$\text{A.}$ 氧分子的质量比氢分子大,所以氧气的压强一定大于氢气的压强
$\text{B.}$ 氧分子的质量比氢分子大,所以氧气的密度一定大于氢气的密度
$\text{C.}$ 氧分子的质量比氢分子大,所以氢分子的速率一定比氧分子的速率大
$\text{D.}$ 氧分子的质量比氢分子大,所以氢分子的方均根速率一定比氧分子的方均根速率
$1 \mathrm{~mol}$ 刚性双原子分子理想气体,当温度为 $T$ 时,其内能为 $($ ) (式中 $R$ 为普适气体常量, $k$ 为玻尔兹曼常量)
$\text{A.}$ ${\frac{3}{2}} R T$
$\text{B.}$ $\frac{3}{2} k T$
$\text{C.}$ $\frac{5}{2} R T$
$\text{D.}$ ${\frac{5}{2}} k T$
两个相同的容器,一个盛氢气,一个盛氦气(均视为刚性分子理想气体),开始时它们的压强和温度都相等,现将6 J热量传给氦气,使之升高到一定温度.若使氢气也升高同样温度,则应向氢气传递热量
$\text{A.}$ 12J
$\text{B.}$ 10J
$\text{C.}$ 6J
$\text{D.}$ 5J
一容器内装有 $N_1$ 个单原子理想气体分子和 $N_2$ 个刚性双原子理想气体分子, 当该系统处在温度为 $T$ 的平衡态时, 其内 能为
$\text{A.}$ $\left(N_1+N_2\right)\left(\frac{3}{2} k T+\frac{5}{2} k T\right)$
$\text{B.}$ ${\frac{1}{2}\left(N_1+N_2\right)}\left(\frac{3}{2} k T+\frac{5}{2} k T\right)$
$\text{C.}$ $N_1 \frac{3}{2} k T+N_2 \frac{5}{2} k T$
$\text{D.}$ $N_1 \frac{5}{2} k T+N_2 \frac{3}{2} k T$
下列各图所示的速率分布曲线,哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线?
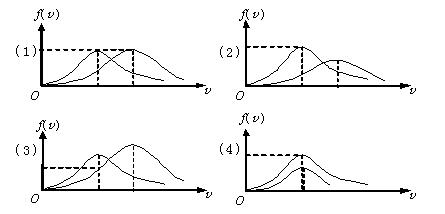
$\text{A.}$ (1)
$\text{B.}$ (2)
$\text{C.}$ (3)
$\text{D.}$ (4)
两种不同的理想气体,若它们的最概然速率相等,则它们的
$\text{A.}$ 平均速率相等,方均根速率相等
$\text{B.}$ 平均速率相等,方均根速率不相等
$\text{C.}$ 平均速率不相等,方均根速率相等
$\text{D.}$ 平均速率不相等,方均根速率不相等
麦克斯韦速率分布曲线如图所示,图中A、B两部分面积相等,则该图表示

$\text{A.}$ $v_0$ 为最概然速率
$\text{B.}$ $v_0$ 为平均速率
$\text{C.}$ $v_0$ 为方均根速率
$\text{D.}$ 速率大于和小于 $\nu_0$ 的分子数各占一半
设某种气体的分子速率分布函数为 $f(v)$, 则速率在 ${ }_{v 1}-{ }_{v 2}$ 区间内的分子的平均速率为
$\text{A.}$ $\int_{v_1}^{v_2} v f(v) \mathrm{d} v$
$\text{B.}$ $v \int_{v_1}^{v_2} v f(v) \mathrm{d} v$
$\text{C.}$ $\int_{v_1}^{v_2} v f(v) \mathrm{d} v / \int_{v_1}^{v_2} f(v) \mathrm{d} v$
$\text{D.}$ $\int_{v_1}^{v_2} f(v) \mathrm{d} v / \int_0^{\infty} f(v) \mathrm{d} v$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
在平衡状态下, 已知理想气体分子的麦克斯韦速率分布函数为 $f(v)$ 、分子质量为 $m$ 、最概然速率为 $v_p$, 试说明下列各式 的物理意义:
(1) $\int_{v_{\nabla}}^{\infty} f(v) \mathrm{d} v$
(2) $\int_0^{\infty} \frac{1}{2} m v^2 f(v) \mathrm{d} v$
已知 $f(v)$ 为麦克斯韦速率分布函数, $v_p$ 为分子的最概然速率. 则 $\int_0^\nu f(v) \mathrm{d} v$
表示 ________ 速率 $v>v_p$ 的分子的平均速率表达式为 ________
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
有 $2 \times 10^{-3} \mathrm{~m}^3$ 刚性双原子分子理想气体, 其内能为 $6.75 \times 10^2 \mathrm{~J}$.
(1)试求气体的压强;
(2)设分子总数为 $5.4 \times 10^{22}$ 个, 求分子的平均平动动能及气体的温度.
(玻尔兹曼常量 $k=1.38 \times 10^{-23} \mathrm{~J} \cdot \mathrm{K}^{-1}$ )
某理想气体的定压摩尔热容为 $29.1 \mathrm{~J} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1}$. 求它在温度为 $273 \mathrm{~K}$ 时分子平均转动动能. (玻尔兹曼常量 $k=1.38 \times 10^{-23} \mathrm{JLK}^{-1}$ )