单选题 (共 10 题 ),每题只有一个选项正确
一个静止的氢离子 $\mathrm{H}^{+}$(氢原子失去一个电子形成的阳离子)在电场中被加速而获得的速 率为一静止的氧离子 $\mathrm{O}^{-2}$ (氧原子失去两个电子形成的阳离子)在同一电场中且通过相同的路 径被加速所获速率的
$\text{A.}$ 2 倍.
$\text{B.}$ $2 \sqrt{2}$ 倍.
$\text{C.}$ 4 倍.
$\text{D.}$ $4 \sqrt{2}$ 倍.
一导体球外充满相对介电常量为 $ \varepsilon$ 的均匀电介质, 若测得导体表面附近场强为 $E$, 则导体球面上的自由电荷面密度 $\sigma$ 为
$\text{A.}$ $\varepsilon_0 E$.
$\text{B.}$ $\left(\varepsilon_0 \varepsilon_r-\varepsilon_0\right) E$.
$\text{C.}$ $\varepsilon_r E$.
$\text{D.}$ $\varepsilon_0 \varepsilon_r E$.
一平行板电容器充电后仍与电源连接, 若用绝缘手柄将电容器两极板间距离拉大, 则极 板上的电荷 $Q$ 、电场强度的大小 $E$ 和电场能量 $W$ 将发生如下变化
$\text{A.}$ $Q$ 减小, $E$ 减小, $W$ 减小.
$\text{B.}$ $Q$ 增大, $E$ 增大, $W$ 增大.
$\text{C.}$ $Q$ 增大, $E$ 减小, $W$ 增大.
$\text{D.}$ $Q$ 增大, $E$ 增大, $W$ 减小.
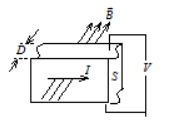
一个通有电流 $I$ 的导体, 厚度为 $D$, 横截面积为 $S$, 放置在磁感 强度为 $B$ 的匀强磁场中, 磁场方向垂直于导体的侧表面, 如图所 示. 现测得导体上下两面电势差为 $V$, 则此导体的霍尔系数等于
$\text{A.}$ $\frac{V D S}{I B}$.
$\text{B.}$ $\frac{I B V}{D S}$.
$\text{C.}$ $\frac{V S}{I B D}$.
$\text{D.}$ $\frac{V D}{I B}$.
在某地发生两件事, 静止位于该地的甲测得时间间隔为 $4 \mathrm{~s}$, 若相对于甲作匀速直线运 动的乙测得时间间隔为 $5 \mathrm{~s}$, 则乙相对于甲的运动速度是 $(c$ 表示真空中光速)
$\text{A.}$ $(4 / 5) \mathrm{c}$.
$\text{B.}$ $(3 / 5) \mathrm{c}$.
$\text{C.}$ $(2 / 5) c$.
$\text{D.}$ $(1 / 5) \mathrm{c}$.
氢原子光谱的巴耳末系中波长最大的谱线用 $\lambda_1$ 表示, 其次波长用 $\lambda_2$ 表示, 则它们的比值 $\lambda_1 / \lambda_2$ 为:
$\text{A.}$ $20 / 27$.
$\text{B.}$ $9 / 8$.
$\text{C.}$ $27 / 20$.
$\text{D.}$ $16 / 9$.
已知粒子在一维矩形无限深势阱中运动, 其归一化波函数为:
$$
\psi(x)=\frac{1}{\sqrt{a}} \cdot \cos \frac{3 \pi x}{2 a}, \quad(-a \leqslant x \leqslant a)
$$
那么粒子在 $x=5 a / 6$ 处出现的概率密度为
$\text{A.}$ $1 /(2 a)$.
$\text{B.}$ $1 / a$.
$\text{C.}$ $1 / \sqrt{2 a}$.
$\text{D.}$ $1 / \sqrt{a}$
有下列四组量子数:
(1) $n=3, l=2, m_l=0, m_s=\frac{1}{2}$
(2) $n=3, l=3, m_l=1, m_s=\frac{1}{2}$.
(3) $n=3, l=1, m_l=-1, m_s=-\frac{1}{2}$.
(4) $n=3, l=0, m_l=0, m_s=-\frac{1}{2}$.
其中可以描述原子中电子状态的
$\text{A.}$ 只有(1)和(3).
$\text{B.}$ 只有 (2)、(3)和(4).
$\text{C.}$ 只有 (2)和(4)
$\text{D.}$ 只有(1)、(3)和(4).
设康普顿效应中入射 $\mathrm{X}$ 射线(伦琴射线)的波长 $\lambda=0.0700 \mathrm{~nm}$, 散射的 $\mathrm{X}$ 射线与入射的 $\mathrm{X}$ 射线垂直, 则反冲电子的动能 $E_K$ 最接近下列哪个值
(电子的静止质量 $m_e=9.11 \times 10^{-31} \mathrm{~kg}$, 普朗克常量 $h=6.63 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}, 1 \mathrm{~nm}=10^{-9} \mathrm{~m}$ )
$\text{A.}$ $7.34 \times 10^{-17} \mathrm{~J}$.
$\text{B.}$ $9.42 \times 10^{-17} \mathrm{~J}$.
$\text{C.}$ $11.53 \times 10^{-17} \mathrm{~J}$.
$\text{D.}$ $12.81 \times 10^{-17} \mathrm{~J}$.
波长 $\lambda=500 \mathrm{~nm}$ 的光沿 $x$ 轴正向传播, 若光的波长的不确定量 $\Delta \lambda=10^{-4} \mathrm{~nm}$, 则利用 不确定关系式 $\Delta p_x \Delta x \geq h$ 可得光子的 $x$ 坐标的不确定量至少为
(普朗克常量 $h=6.63 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}$ )
$\text{A.}$ $25 \mathrm{~cm}$
$\text{B.}$ $50 \mathrm{~cm}$
$\text{C.}$ $250 \mathrm{~cm}$
$\text{D.}$ $500 \mathrm{~cm}$
填空题 (共 10 题 ),请把答案直接填写在答题纸上
已知某静电场的电势函数 $U=6 x-6 x^2 y-7 y^2(\mathrm{SI})$. 由场强与电势梯度的关系 式可得点 $(1,1,0)$ 处的电场强度 $\vec{E}=$ $\vec{i}$ ________ $\vec{j} $ ________ $\vec{k} $ ________
如图所示, 两块很大的导体平板平行放置, 面积都是 $S$, 有一定厚 度, 带电荷分别为 $Q_1$ 和 $Q_2$. 如不计边缘效应, 则 $A 、 C$ 两个表面上的 电荷面密度分别为 ________ 和 ________

一个带电的金属球, 当其周围是真空时, 储存的静电能量为 $W_0$, 使其电荷保持不变, 把它浸没在相对介电常墨为 $\&$ 的无限大各向同性均匀电介质中, 这时它的静电能量 $W=$ ________ $W_0$.
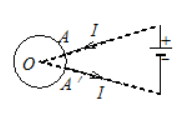
如图, 两根导线沿半径方向引到半径为 $R$ 的均质铁圆环上 的 $A 、 A^{\prime}$ 两点, 并在很远处与电源相连, 设 $\angle A O A^{\prime}=45^{\circ}$, 则 环中心的磁感强度为
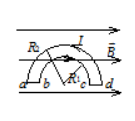
半径分别为 $R_1$ 和 $R_2$ 的两个半圆弧与直径的两小段构成的通电 线圈 $a b c d a$ (如图所示), 放在磁感强度为 $\bar{B}$ 的均匀磁场中, $\bar{B}$ 平行 线圈所在平面. 则线圈受到的磁力矩为
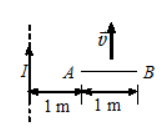
如图, 一无限长直导线中通电流 $I$, 右侧有一长为 $1 \mathrm{~m}$ 的金 属棒与导线垂直共面。棒的最左端 $\mathrm{A}$ 与长直导线相距为 $1 \mathrm{~m}$, 当 棒以速度 $v$ 平行于长直导线匀速运动时, 棒产生的动生电动势为
一线圈中的电流为 $1 \mathrm{~A}$, 在 $\frac{1}{16} \mathrm{~s}$ 内均匀地减小到零, 所产生的自感电动势为 $8 \mathrm{~V}$, 此线圈 的自感为 H.
加在平行板电容器极板上的电压变化率 $1.0 \times 10^6 \mathrm{~V} / \mathrm{s}$, 在电容器内产生 $2 \mathrm{~A}$ 的位移电流, 则该电容器的电容量为 $\mu \mathrm{F}$.
一根导线长为 $0.2 \mathrm{~m}$, 载有电流 $3 \mathrm{~A}$, 放在磁感应强度为 $10 \mathrm{~T}$ 的均匀磁场中, 并与磁场 成 $30^{\circ}$ 角, 则导线受到的磁力为 N.
当氢原子中的电子处于 $n=3, l=2$ 的状态时, 该电子的轨道角动量有 个可能的空 间取向。
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图, 用绝缘细线弯成的半圆环, 半径为 $R$, 其上均匀地带 有正电荷, 电荷线密度为 $\lambda$, $\lambda$ 为一常数。试求圆心 $O$ 点的电场 强度的大小及方向.
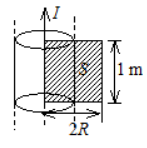
一无限长圆柱形铜导体(磁导率 $\left.\mu_0\right)$, 半径为 $R$, 通有均匀分布 的电流 $I$. 今取一施形平面 $S$ (长为 $1 \mathrm{~m}$, 宽为 $2 R$ ), 位置如右图中画 斜线部分所示, 求
(1) 铜导体内外磁场的分布;
(2) 通过该阴影矩形平面的磁通量。
在惯性系 $S$ 中, 两事件发生在同一地点而时间相隔为 8 秒, 另一惯性系 $S^{\prime}$ 以速度 $v=0.6 c$ 相对于 $S$ 运动, 则 $S^{\prime}$ 系中测得的两事件的空间间隔是多少?
如图所示, 一半径为 $r_2$ 电荷线密度为 $\lambda$ 的均匀带电圆环, 里边 有一半径为 $r_1$ 总电阻为 $R$ 的导体环, 两环共面同心 $\left(r_2 \gg r_1\right)$, 当大 环以变角速度 $\omega=\omega(t)$ 绕垂直于环面的中心轴旋转时, 求小环中的感 应电流.

假如电子运动速度与光速可以比拟, 则当电子的动能等于它静止能量的 2 倍时, 其德布 罗意波长为多少?
(普朗克常量 $h=6.63 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}$, 电子静止质量 $m_{\varepsilon}=9.11 \times 10^{-31} \mathrm{~kg}$ )