单选题 (共 15 题 ),每题只有一个选项正确
关于高斯定理, 以下说法正确的是
$\text{A.}$ 高斯定理是普遍适用的, 但用它计算电场强度时要求电荷分布具有某种 对称性;
$\text{B.}$ 高斯定理对非对称性的电场是不正确的;
$\text{C.}$ 高斯定理一定可以用于计算电荷分布具有对称性的电场的电场强度;
$\text{D.}$ 高斯定理一定可以用于计算非对称性电荷分布的电场的电场强度。
如图 1 所示, 半径为 $R$ 的均匀带电球面, 总电量为 $Q$, 设无穷远处的电势为零, 则球内距离球心为 $r$ 的 $P$ 点处的电场强度的大小和电势为

$\text{A.}$ $E=0, U=Q / 4 \pi \varepsilon \circ R$;
$\text{B.}$ $E=0, U=Q / 4 \pi \varepsilon_0 r$;
$\text{C.}$ $E=Q / 4 \pi \varepsilon_0 r^2, \quad U=Q / 4 \pi \varepsilon_0 r$;
$\text{D.}$ $E=Q / 4 \pi \varepsilon_0 r^2, U=Q / 4 \pi \varepsilon_0 R$ 。
以下说法错误的是
$\text{A.}$ 电荷电量大, 受的电场力可能小;
$\text{B.}$ 电荷电量小, 受的电场力可能大;
$\text{C.}$ 电场为零的点, 任何点电荷在此受的电场力为零;
$\text{D.}$ 电荷在某点受的电场力与该点电场方向一致。
关于感生电场, 下列说法正确的是
$\text{A.}$ 感生电场对静止电荷没有电场力的作用;
$\text{B.}$ 感生电场是保守场。
$\text{C.}$ 感生电场的电场线不是闭合线。
$\text{D.}$ 感生电场不能引入电势的概念。
当平行板电容器板间为真空时, 其电容为 $C_0$, 板间场强为 $E_0$, 电位移为 $D_0$ 。 如充电后将电源断开, 再充满相对介电常数为 $\varepsilon_r$ 的电介质, 则电容、场强以及电位 移的大小分别为
$\text{A.}$ $\varepsilon_r C_0, E_0 / \varepsilon_r, D_0$;
$\text{B.}$ $\varepsilon_r C_0, E_0, \varepsilon_r D_0$;
$\text{C.}$ $\varepsilon_r C_0 \quad E_0 \quad D_0 / \varepsilon_r$;
$\text{D.}$ $C_0 \quad E_0 \quad D_0$ 。
若要使半径为 $4 \times 10^{-3} \mathrm{~m}$ 的裸铜线表面的磁感应强度为 $6.0 \times 10^{-5} \mathrm{~T}$, 其铜线中 需要通过的电流为
$\text{A.}$ $0.12 \mathrm{~A}$;
$\text{B.}$ $12 \mathrm{~A}$;
$\text{C.}$ $1.2 \mathrm{~A}$;
$\text{D.}$ $2.4 \mathrm{~A}$ 。
两根长直导线通有电流 I, 如图 2 所示, 有两个回路, 则有
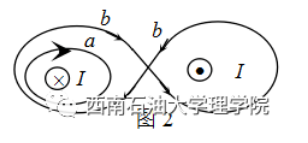
$\text{A.}$ $\oint_a \vec{B} \bullet d \vec{l}=-\mu_0 I$
$\text{B.}$ $\oint_a \vec{B} \bullet d \vec{l}=\mu_0 I$
$\text{C.}$ $\oint_b \vec{B} \bullet d \vec{l}=\mathbf{0}$
$\text{D.}$ $\oint_b \vec{H} \bullet d \vec{l}=\mathbf{2} \mu_0 I$
两电容器的电容之比 $C_1: C_2=1: 4$, 如果它们充的电量相等, 则两电容器储存 的电场能之比为
$\text{A.}$ $1: 4$;
$\text{B.}$ $4: 1$;
$\text{C.}$ $2: 1$;
$\text{D.}$ $1: 2$ 。
关于温度的意义, 下列几种说法中错误的是
$\text{A.}$ 气体的温度是分子平动动能的量度;
$\text{B.}$ 气体的温度是大量气体分子热运动的集体表现, 具有统计意义;
$\text{C.}$ 温度的高低反映物质内部分子运动剧烈程度的不同;
$\text{D.}$ 从微观上看, 气体的温度表示每个气体分子的冷热程度。
气缸内盛有一定量的氢气 (可视作理想气体), 当温度不变而压强增大一倍时, 氢气分子的平均碰撞次数 $\bar{Z}$ 和平均自由程 $\bar{\lambda}$ 的变化情况是
$\text{A.}$ $\bar{Z}$ 和 $\bar{\lambda}$ 都增大一倍;
$\text{B.}$ $\bar{Z}$ 和 $\bar{\lambda}$ 都减为原来的一半;
$\text{C.}$ $\bar{Z}$ 增大一倍而 $\bar{\lambda}$ 减为原来的一半;
$\text{D.}$ $\bar{Z}$ 减为原来的一半陑 $\bar{\lambda}$ 增大一倍。
对同一种理想气体, 在同一温度下, 最概然速率 $v_p$ 、平均速率 $\bar{v}$ 以及方均根速 率 $\sqrt{v^2}$ 之间的关系, 正确的为
$\text{A.}$ $\sqrt{\overline{v^2}}>v_p>\bar{v}$
$\text{B.}$ $\sqrt{\overline{v^2}}>\bar{v} > v_p$
$\text{C.}$ $ v_p > \sqrt{\overline{v^2}}>\bar{v} $
$\text{D.}$ $ v_p > \bar{v} > \sqrt{\overline{v^2}} $
一卡诺热机的高温热源和低温热源温度分别为 $527^{\circ} \mathrm{C}$ 和 $227^{\circ} \mathrm{C}$, 热机在最大 效率下工作, 每一循环吸热 $1600 \mathrm{~J}$, 此热机每一循环对外做功
$\text{A.}$ $200 \mathrm{~J}$;
$\text{B.}$ $300 \mathrm{~J}$;
$\text{C.}$ $400 \mathrm{~J}$;
$\text{D.}$ $600 \mathrm{~J}$;
一定量的理想气体向真空作绝热自由憉胀, 体积由 $V_1$ 增至 $V_2$, 在此过程中气 体的
$\text{A.}$ 内能不变, 熵增加;
$\text{B.}$ 内能不变, 熵减少;
$\text{C.}$ 内能增加, 熵增加;
$\text{D.}$ 内能不变, 熵不变。
恒定磁场中有一载流圆线圈, 若线圈的半径增大一倍, 且其中电流减小为原来 的一半, 磁场强度变为原来的 2 倍, 则该线圈所受的最大磁力矩是原来线圈的最大磁力矩的
$\text{A.}$ 1倍
$\text{B.}$ 2倍
$\text{C.}$ 4倍
$\text{D.}$ 8倍
自感系数 $L=0.4 \mathrm{H}$ 的螺线管中通以 $I=9 \mathrm{~A}$ 的电流时, 螺线管存储的磁场能量为
$\text{A.}$ $16.2 \mathrm{~J}$;
$\text{B.}$ $8.1 \mathrm{~J}$;
$\text{C.}$ $32.4 \mathrm{~J}$;
$\text{D.}$ $64.4 \mathrm{~J}$;
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图 3 所示, 两个同轴均匀带电长直金属圆柱面, 内外筒半径 分别为 $R_1$ 和 $R_2$, 两筒间为空气, 沿轴线方向上单位长度电量分别为 $\lambda_1$ 和 $\lambda_2$ 。求:
(1)两圆柱面之间的电场强度;
(2) 两圆柱面之间的电势差。

一个负电子以速度 $\vec{v}=5 \times 10^5 \vec{i}(\mathrm{~m} / \mathrm{s})$ 通过磁感强度为 $\vec{B}=6 \vec{i}+0.2 \vec{j}(\mathrm{~T})$ 的磁场中某点处时, 求 该磁场作用于负电子的洛伦兹力 $\vec{f}$ 。
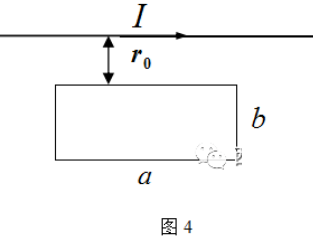
静止的矩形导体线框与长直载流导线共面, 已知线框的长和宽 分别为 $a$ 和 $b$, 距载流导线距离为 $r_0$, 如图 4 所示, 电流 $I=I_m \sin (\omega t)$, 求:
(1) 通过矩形线框的磁通量;
(2) 矩形线框中的电动势 $\boldsymbol{\varepsilon}$ 。
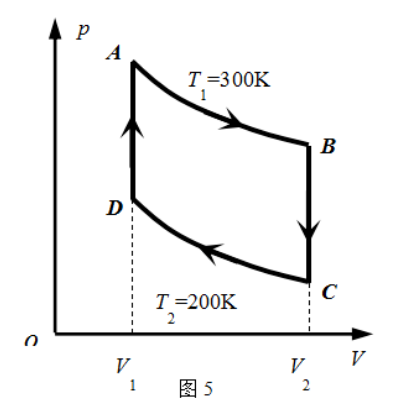
有 $3.2 \times 10^{-2} \mathrm{~kg}$ 氧气作 $\mathrm{ABCDA}$ 循环过程, 加图 5 所示, $\mathrm{A} \rightarrow \mathrm{B}$ 和 $\mathrm{C} \rightarrow \mathrm{D}$ 都为等温过程, 设 $T_1=300 \mathrm{~K}, \mathrm{~T}_2=200 \mathrm{~K}, \mathrm{~V}_2=2 \mathrm{~V}_1$ 。 求 (1) $\mathrm{A} \rightarrow \mathrm{B} 、 \mathrm{~B}$ $\rightarrow \mathrm{C} 、 \mathrm{C} \rightarrow \mathrm{D} 、 \mathrm{D} \rightarrow \mathrm{A}$ 各个过程系统吸收的热量 ; (2) 系统完成一次循环所作的净 功; (3) 此循环的效率。
一容器储有多原子分子气体, 可视为理想气体, 该气体分子质量 $\mathrm{m}=3.0 \times 10^{-26} \mathrm{~kg}$, 其压强为一个标准大气压, 温度为 $t=27^{\circ} \mathrm{C}$ 。求: (1) 该气体分子 的方均根速率; (2) 该气体的质量密度 $\rho$; (3) 该气体分子的平均动能。
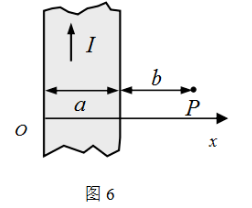
如图 6 所示, 有一无限长通有电流的薄导体平板, 宽度为 $a$, 电 流 $I$ 在板上均匀流过, $P$ 点与导体板共面, 距其右边缘距离为 $b$ 。求: $P$ 点的磁感 强度 $B$ 的大小。
常温常压下, 空气分子平均速率约 500 米/秒, 如果老师在讲台 打开香水瓶, 教室后面学生不能马上闻到香水味, 为什么? 请说明理由。