单选题 (共 10 题 ),每题只有一个选项正确
在升降机天花板上栓有轻绳,其下端系一重物,当升降机以加速度 $\mathrm{a}$ 上升时, 绳中的张力正好等于绳子所能承受的最大张力的一半, 问 升降机以多大加速度上升时,绳子刚好被拉断?

$\text{A.}$ $2 \mathrm{a}$
$\text{B.}$ 2 $(\mathrm{a}+\mathrm{g})$
$\text{C.}$ $2 a+g$
$\text{D.}$ $a+g$
质量为 $\mathrm{M}=1 \mathrm{~kg}$ 的物体, 用一根长为 $l=1 m$ 的细绳悬挂在天花板上。 今有一质量为 $\mathrm{m}=10 \mathrm{~g}$ 的子弹以 $\mathrm{v}_0=1000 \mathrm{~m} / \mathrm{s}$ 的水平速度射穿物体, 刚穿出物侇时子弹的速度大小 $\mathrm{v}=200 \mathrm{~m} / \mathrm{s}$, 设穿透时间极短, 则子 弹刚穿出时绳中张力为

$\text{A.}$ $74 \mathrm{~N}$
$\text{B.}$ $64 \mathrm{~N}$
$\text{C.}$ $144 \mathrm{~N}$
$\text{D.}$ $154 \mathrm{~N}$
一刚体以每分钟 60 转绕 Z 轴作匀速转动( $\vec{\omega}$ 沿 Z 轴正方向). 设某时刻刚体上一点 $\mathrm{P}$ 的位置矢量为 $\vec{r}=3 \vec{i}+4 \vec{j}+5 \vec{k}$, 其单位为 “ $10^{-2} \mathrm{~m}$ ”, 若以 “ $10^{-2} \mathrm{~m} / \mathrm{s}$ ”为速度单位, 则该 时刻 $P$ 点的速度为:
$\text{A.}$ $\vec{v}=94.2 \vec{i}+125.6 \vec{j}+157.0 \vec{k}$
$\text{B.}$ $\vec{v}=-25.1 \vec{i}+18.8 \vec{j}$
$\text{C.}$ $\vec{v}=-25.1 \vec{i}-18.8 \vec{j}$
$\text{D.}$ $\vec{v}=31.4 \vec{k}$
正方形的两对角上, 各置电荷 $\mathrm{Q}$, 在另两对角上各置电荷 $\mathrm{q}$. 若 $\mathrm{Q}$ 所受合力为零, 则 $\mathrm{Q}$ 与 $\mathrm{q}$ 的关系为
$\text{A.}$ $Q=-2 \sqrt{2} q$
$\text{B.}$ $\mathrm{Q}=-\sqrt{2} \mathrm{q}$
$\text{C.}$ $\mathrm{Q}=-4 \mathrm{q}$
$\text{D.}$ $Q=-2 \mathrm{q}$
半径为 $\mathrm{R}$ 的水平平台可以绕通过其中心的坚惪光滑固定轴自由转动, 相应转动惯 量为 $\mathrm{J}$ 。质量为 $\mathrm{m}$ 的小孩站在平台边缘上,平台和小孩开始时均静止。小孩突然 相对平台以 $\mathrm{v}$ 的速率在台边缘沿逆时针转向走动时, 则此平台相对地面旋转的角 速度和遈转方向分别为
$\text{A.}$ $\omega=\frac{m R v}{J+m R^2}$, 逆时针
$\text{B.}$ $\omega=\frac{m R v}{J}$, 逆时针
$\text{C.}$ $\omega=\frac{m R v}{J}$, 顺时针
$\text{D.}$ $\omega=\frac{m R v}{J+m R^2}$, 顺时计
一点电荷在静电场中的某点所受的电场力为零, 则该点
$\text{A.}$ 场强一定为零, 电势一定为零
$\text{B.}$ 场强不一定为零、电势一定为零
$\text{C.}$ 场强不一定为零, 电势不一定为零
$\text{D.}$ 场强一定为零, 电势不一定为零
将一个带电量为 $\mathrm{q}$ 的点电荷放在一个半径为 $\mathrm{r}$ 的导体球附近, 点电荷距离导体球球 心为 $d(d>r)$ ,则
$\text{A.}$ 点电荷在球内各点所产生的电场强度大小相同:
$\text{B.}$ 感应电荷在球心产生的电场强度大小为 $\frac{q}{4 \pi \varepsilon_0 r^2}$ ;
$\text{C.}$ 感应电荷在球心产生的电场强度大小为 $\frac{q}{4 \pi \varepsilon_0 d^2}$ :
$\text{D.}$ 感应电荷在球内各点所产生的电场强度大小相同。
两个半径为 $\mathrm{R}$ 的相同金属环相互垂直放置, 两接触点都绝缘, 通 过相同的电流, 电流的方向如图, 真空时环心 $O$ 处磁感应强度的 大小为

$\text{A.}$ $\frac{\mu_0 I}{2 R}$
$\text{B.}$ $\frac{\mu_0 I^2}{2 R}$
$\text{C.}$ $\sqrt{2} \frac{\mu_0 I}{2 R}$
$\text{D.}$ $\sqrt{2} \frac{\mu_0 I^2}{2 R}$
如图, 无限长载流直导线与矩形载流线圈在同一平面内, 若长 直导线固定不动, 则矩形载流线框将
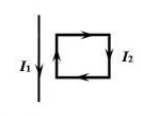
$\text{A.}$ 转动:
$\text{B.}$ 不动;
$\text{C.}$ 向着长直导线平移;
$\text{D.}$ 离开长直导线平移。
磁介质有三种,用相对磁导䔞 $\mu_x$ 描述它们的各自的特性时
$\text{A.}$ 顺磁质 $\mu_r>0$, 抗磁质 $\mu_x < 0$, 铁磁质 $\mu_x>>1$.
$\text{B.}$ 顺磁质 $\mu_r>1$, 抗磁质 $\mu_x=1$, 铁磁质 $\mu_x>>1$.
$\text{C.}$ 顺磁质 $\mu_{\mathrm{r}}>1$, 抗磁质 $\mu_x < 1$, 铁磁质 $\mu_x>>1$.
$\text{D.}$ 顺磁质 $\mu_r>0$, 抗磁质 $\mu_x < 0$, 铁䃍质 $\mu_x>1$.
填空题 (共 10 题 ),请把答案直接填写在答题纸上
一运动质点的速率 $v$ 与路程 $s$ 的关系为 $v=1+s^2$ (SI). 则其切向加速度以 $S$ 来表达 的表达式为: $a t=$
一船员站在甲船上, 船员与甲船的总质量为 $300 \mathrm{~kg}$, 他用的水平力 $200 \mathrm{~N}$ 拉一轻 绳, 轻绳的另一端系在质量为 $200 \mathrm{~kg}$ 的乙船上。开始时两船都静止, 若不计水的 阻力, 则在开始拉动后的前 $2 s$ 内, 站在甲船上的船员所作的功为
真空中有一均匀带电球体, 半径为 $R$, 所带电荷为 $Q$ 。球面外 $A 、 B$ 两点到球心 $O$ 点的距离分别为 $r_1$ 和 $r 2$, 将检验电荷 $q q$ 点 $A$ 移到点 $B$ 电场力所做的功为
$A, B$ 两个导体球,它们的半径之比为 $2: 1, A$ 球带正电荷 $Q, B$ 球不带电. 若使两球接触 一下再分离,当 $A, B$ 两球相距为 $R$ 时 ( $R$ 远大于两球半径, 以致于可认为 $A, B$ 是点电 荷), 则两球间的静电力 $\mathrm{F}=$
带电粒子沿垂直于磁感线的方向飞入有介质的匀强磁场中.由于粒子和磁场中的 物质相互作用, 损失了自己原有动能的一半。路径起点的轨道曲率半径与路径终 点的轨道曲率半径之比为 $R_1: R_2=$
如图, 直角三角形与一长直载流导线共面, 其一直角边与 长直导线垂直, 已知电流 $I$, 三角形高为 $\mathrm{h}$, 底边长为 $a$, 它与长直导线的最小距离为 $b$ 。求三角形面积内的磁通 量
一载有电流 $I$ 的细导线分别均匀密绕在半径为 $R$ 和 $r$ 的长直圆筒上形成两个螺线 㖕 $(R=2 r)$, 两螺线管单位长度上的匜数相等, 两螺线管中的磁感应强度大小 $B_R$ 和 $B_r$ 的比值 $B_R: B_r=$
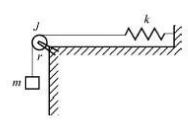
如图,已知滑轮的半径为 $r$, 转动惯量为 $J$,弹簧的倔强系数 $k$. 设开始时物㤓静止且弹簧无伸长, 问质量为 $m$ 的 物体落下 $h$ 时的速率 $v=$
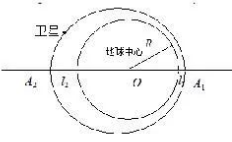
一颗人造卫星绕地球沿椭圆轨道运行, 地球 的中心 $O$ 为该椭圆的一个焦点。已知地球半 径 $\mathrm{R}=6378 \mathrm{~km}$, 卫星与地面的最近距离 $l_1=439 \mathrm{~km}$, 与地面的最远距离 $l_2=2384 \mathrm{~km}$ 。 若卫星在近地点 $\mathrm{A} 1$ 的角速度 $\omega_1=1.2 \mathrm{rad} / \mathrm{s}$, 则卫星在远地点 $\mathrm{A}_2$ 的角速度 $\omega_2=$
一空气平行板电容器, 极板间距为 $\mathrm{d}$, 电容为 $\mathrm{C}$ 。若 在两板中间平行地揷入一块厚度为 $\mathrm{d} / 3$ 的金属板, 则 其电容值变为

解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图所示, 劲度系数为 $\mathrm{k}$ 的弹簧, 一端固定于墙上, 另一端与质量 为 $m_1$ 的木块相接, $m_1$ 又与质量为 $m_2$ 的木块紧靠在一起, 整个系统放在光滑水 平面上。现在以向右不变的力 $\mathrm{F}$ 施加在 $\mathrm{m}_2$ 上, 使自平衡位置由静止开始运动。 求木块 $\mathrm{m}_1 、 \mathrm{~m}_2$ 所受合外力为零时的速度, 以及此过程中 $\mathrm{m}_2$ 对 $\mathrm{m}_1$ 所作的功, 恒 力 $\mathrm{F}$ 对 $\mathrm{m}_2$ 所作的功。

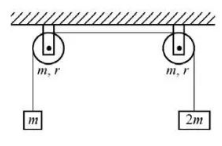
一轻绳跨过两个质量均为 $\mathrm{m}$, 半径均 为 $\mathrm{r}$ 的均匀圆盘状定滑轮,绳的两端分别挂着质量 分别为 $\mathrm{m}$ 和 $2 \mathrm{~m}$ 的重物, 如图所示,绳与滑轮间无相 对滑动,滑轮轴光滑,两个定滑轮的转动惯量均为 $\mathrm{mr}^2 / 2$. 将由两个定滑轮以及质量为 $\mathrm{m}$ 和 $2 \mathrm{~m}$ 的重物 组成的系统从静止释放, 求三段绳内的张力
证明题: 电荷 $\mathrm{Q}$ 均匀分布在半径为 $R$ 的球体内,设无穷远处为电势零 点, 试证明距离球心 $r( < R)$ 处的电势为
$$
\mathrm{U}=\mathrm{Q}\left(3 \mathrm{R}^2-\mathrm{r}^2\right) / 8 \pi \varepsilon_0 \mathrm{R}^3
$$
两块“无限大”均匀带电导体相互平行放置, 设 四个表面的电荷面密度分别为 $\sigma_1, \sigma_2, \sigma_3, \sigma_4$, 如图所示. 求 证当静电平衡时: $\sigma_2=-\sigma_3, \sigma_1=\sigma_4$.

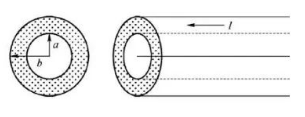
一根无限长载流导体的 直圆管, 内外半径分别为 $\mathrm{a}$ 和 $\mathrm{b}$, 电流 I 沿轴线方向流动, 并均匀地分布管壁 的截面上, 空间某点到轴线的距离为 $r$, 求该点磁感强度的大小.