单选题 (共 4 题 ),每题只有一个选项正确
若随机变量 $X \sim B\left(5, \frac{1}{3}\right)$ ,则 $P(X=3)$ 等于
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{40}{243}$
$\text{C.}$ $\frac{10}{27}$
$\text{D.}$ $\frac{3}{5}$
袋中装有 2 个红球, 3 个黄球,有放回地抽取 3 次,每次抽取 1 球,则 3 次中恰有 2 次抽到黄球的概率是( )
$\text{A.}$ $\frac{2}{5}$
$\text{B.}$ $\frac{3}{5}$
$\text{C.}$ $\frac{18}{125}$
$\text{D.}$ $\frac{54}{125}$
从装有 3 个白球、 4 个红球的箱子中,随机取出了 3 个球,恰好是 2 个白球、 1 个红球的概率是(
$\text{A.}$ $\frac{4}{35}$
$\text{B.}$ $\frac{6}{35}$
$\text{C.}$ $\frac{12}{35}$
$\text{D.}$ $\frac{36}{343}$
在 $n\left(n \in N^*\right)$ 次独立重复试验中,每次试验的结果只有 $A, B, C$ 三种,且 $A$ ,
$B, C$ 三个事件之间两两互斥.已知在每一次试验中,事件 $A, B$ 发生的概率均为 $\frac{2}{5}$ ,则事件 $A, B, C$ 发生次数的方差之比为( )
$\text{A.}$ $5: 5: 4$
$\text{B.}$ $4: 4: 3$
$\text{C.}$ 3:3: 2
$\text{D.}$ 2:2: 1
多选题 (共 1 题 ),每题有多个选项正确
若随机变量 $X \sim B\left(10, \frac{2}{3}\right)$ ,下列说法中正确的是
$\text{A.}$ $P(X=3)= C _{10}^3\left(\frac{1}{3}\right)^3\left(\frac{2}{3}\right)^7$
$\text{B.}$ 期望 $E(X)=\frac{20}{3}$
$\text{C.}$ 期望 $E(3 X+2)=22$
$\text{D.}$ 方差 $D(3 X+2)=20$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
已知随机变量 $X: B (6, p )$ ,且 $E(X)=3$ ,则 $P(X=1)=$
随机变量 $X \sim B\left(2, \frac{1}{3}\right)$ ,则 $\sigma(2 X+1)=$
现有 7 张卡片,分别写上数字 $1,2,2,3,4,5,6$ .从这 7 张卡片中随机抽取 3 张,记所抽取卡片上数字的最小值为 $\xi$ ,则 $P(\xi=2)=$ $\qquad$ ,$E(\xi)=$ $\qquad$
甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为 $\frac{5}{6}$ 和 $\frac{3}{5}$ ,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 $\qquad$ ; 3 次活动中,甲至少获胜 2 次的概率为 $\qquad$ .
在 4 次独立试验中,事件 A 出现的概率相同,若事件 A 至少发生 1 次的概率是 $\frac{65}{81}$ ,则事件 A 在一次试验中出现的概率是 $\qquad$
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某工厂的某种产品成箱包装,每箱 200 件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品。检验时,先从这箱产品中任取 20 件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为 $p(0 < p < 1)$ ,且各件产品是否为不合格品相互独立.
(1)记 20 件产品中恰有 2 件不合格品的概率为 $f(p)$ ,求 $f(p)$ 的最大值点 $p_0$ ;
(2)现对一箱产品检验了 20 件,结果恰有 2 件不合格品,以(1)中确定的 $p_0$ 作为 $p$ 的值.已知每件产品的检验费用为 2 元,若有不合格品进入用户手中,则工厂要对每件不合格品支付 25 元的赔偿费用.
(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为 $X$ ,求 $E X$ ;
(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
已知一个射手每次击中目标的概率为 $P =\frac{3}{5}$ ,求他在 4 次射击中下列事件发生的概率.
(1)命中一次;
(2)命中两次.
已知一个射手每次击中目标的概率为 $P =\frac{3}{5}$ ,求他在 4 次射击中下列事件发生的概率.求:
(1)恰在第三次命中目标的概率;
(2)刚好在第二次、第三次两次击中目标的概率.
已知一个射手每次击中目标的概率为 $P =\frac{3}{5}$ ,求他在 4 次射击中下列事件发生的概率.求:
(1)至少命中一次的概率;
(2)至多命中两次的概率.
学习强国中有两项竞赛答题活动,一项为"双人对战",另一项为"四人赛".活动规则如下:一天内参与"双人对战"活动,仅首局比赛可获得积分,获胜得 2 分,失败得 1 分;一天内参与"四人赛"活动,仅前两局比赛可获得积分,首局获胜得 3 分,次局获胜得 2 分,失败均得 1 分.已知李明参加"双人对战"活动时,每局比赛获胜的概率为 $\frac{1}{2}$ ;参加"四人赛"活动(每天两局)时,第一局和第二局比赛获胜的概率分别为 $p, \frac{1}{3}$ .李明周一到周五每天都参加了"双人对战"活动和"四人赛"活动(每天两局),各局比赛互不影响。
(1)求李明这 5 天参加"双人对战"活动的总得分 $x$ 的分布列和数学期望;
(2)设李明在这 5 天的"四人赛"活动(每天两局)中,恰有 3 天每天得分不低于 3 分的概率为 $f(p)$ .求 $p$ 为何值时,$f(p)$ 取得最大值.
袋中有 8 个球,其中 5 个黑球, 3 个红球,从袋中任取 3 个球,求取出的红球数 X 的分布列,并求至少有一个红球的概率.
袋中有 8 个球,其中 5 个黑球, 3 个红球,从袋中任取 3 个球,求取出的黑球数 X 的分布列.
一机床生产了 100 个汽车零件,其中有 40 个一等品、 50 个合格品、 10 个次品,从中随机地抽出 4 个零件作为样本.用 $X$ 表示样本中一等品的个数.
(1)若有放回地抽取,求 $X$ 的分布列;
(2)若不放回地抽取,用样本中一等品的比例去估计总体中一等品的比例.
① 求误差不超过 0.2 的 $X$ 的值;
② 求误差不超过 0.2 的概率(结果不用计算,用式子表示即可)
唐三彩是中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有 1300 多年的历史,制作工艺十分复杂,而且优质品检验异常严格,检验方案是:先从烧制的这批唐三彩中任取 3 件作检验,这 3 件唐三彩中优质品的件数记为 $n$ ,如果 $n=2$ ,再从这批唐三彩中任取 3 件作检验,若都为优质品,则这批唐三彩通过检验:如果 $n=3$ ,再从这批唐三彩中任取 1 件作检验,若为优质品,则这批唐三彩通过检验,其他情况下,这批唐三彩的优质品概率为 $\frac{1}{3}$ ,即取出的每件唐三彩是优质品的概率都为 $\frac{1}{3}$ ,且各件唐三彩是否为优质品相互独立.
(1)求这批唐三彩通过优质品检验的概率;
(2)已知每件唐三彩的检验费用为 100 元,且抽取的每件唐三彩都需要检验,对这批唐三彩作质量检验所需的总费用记为 $X$ 元,求 $X$ 的分布列及数学期望.
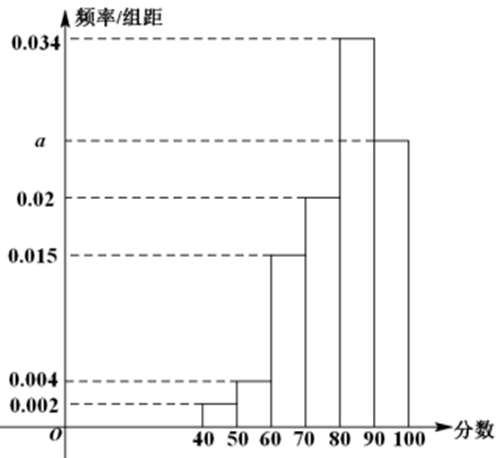
近平总书记在党的十九大报告中指出,保障和改善人民最关心最直接最现实的利益问题要从"让人民群众满意的事情"做起。2021年底某市城市公园建设基本完成,为了解市民对该项目的满意度,从该市随机抽取若干市民对该项目进行评分(满分 100 分),绘制成如图所示的频率分布直方图,并将分数从低到高分为四个等级: