单选题 (共 7 题 ),每题只有一个选项正确
已知 $a=2^{\frac{4}{3}}, b=4^{\frac{2}{5}}, c=25^{\frac{1}{3}}$ ,则
$\text{A.}$ $b < a < c$
$\text{B.}$ $a < b < c$
$\text{C.}$ $b < c < a$
$\text{D.}$ $c < a < b$
若幂函数 $f(x)=\left(m^2-4 m+4\right) \cdot x^{m^2-6 m^{+} 8}$ 在 $(0,+\infty)$ 上为增函数,则 $m$ 的值为
$\text{A.}$ 1 或 3
$\text{B.}$ 1
$\text{C.}$ 3
$\text{D.}$ 2
若二次函数 $g(x)$ 满足 $g(1)=1, g(-1)=5$ ,且图象过原点,则 $g(x)$ 的解析式为
$\text{A.}$ $g(x)=2 x^2-3 x$
$\text{B.}$ $g(x)=3 x^2-2 x$
$\text{C.}$ $g(x)=3 x^2+2 x$
$\text{D.}$ $g(x)=-3 x^2-2 x$
若二次函数 $y=k x^2-4 x+2$ 在区间 $[1,2]$ 上是单调递增函数,则实数 $k$ 的取值范围为( )
$\text{A.}$ $[2,+\infty)$
$\text{B.}$ $(2,+\infty)$
$\text{C.}$ $(-\infty, 0)$
$\text{D.}$ $(-\infty, 2)$
若 $a=(2)^{\frac{2}{3}}, b=3^{\frac{2}{3}}, c=\left(\frac{1}{2}\right)^{\frac{2}{3}}, d=\left(\frac{1}{3}\right)^{\frac{2}{3}}$ ,则 $a, b, c, a$ 的大小关系是
$\text{A.}$ $a>b>c>d$
$\text{B.}$ $b>a>d>c$
$\text{C.}$ $b>a>c>d$
$\text{D.}$ $a>b>d>c$
已知函数 $f(x)$ 是定义在 R 上的偶函数,当 $x \geqslant 0$ 时,$f(x)=x^2-4 x$ ,则不等式 $f(x+2) < 5$ 的解集为
$\text{A.}$ $(-3,7)$
$\text{B.}$ $(-4,5)$
$\text{C.}$ $(-7,3)$
$\text{D.}$ $(-2,6)$
满足 $(m+1)^{-\frac{1}{3}} < (3-2 m)^{-\frac{1}{3}}$ 的实数 $m$ 的取值范围是()。
$\text{A.}$ $\left(\frac{2}{3}, \frac{3}{2}\right)$
$\text{B.}$ $\left(-\infty, \frac{2}{3}\right) \cup\left(1, \frac{3}{2}\right)$
$\text{C.}$ $\left(\frac{2}{3},+\infty\right)$
$\text{D.}$ $(-\infty,-1) \cup\left(\frac{2}{3}, \frac{3}{2}\right)$
多选题 (共 2 题 ),每题有多个选项正确
如图是二次函数 $y=a x^2+b x+c(a \neq 0)$ 图象的一部分,图象过点 $A(-3$ , 0 ),对称轴为 $x=-1$ .给出下面四个结论正确的为
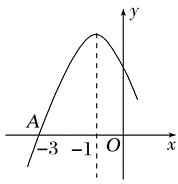
$\text{A.}$ $b^2>4 a c$
$\text{B.}$ $2 a-b=1$
$\text{C.}$ $a-b+c=0$
$\text{D.}$ $5 a < b$
已知函数 $f(x)=\left|x^2-2 a x+b\right|(x \in R )$ ,给出下列命题,其中是真命题的是
$\text{A.}$ 若 $a^2-b \leqslant 0$ ,则 $f(x)$ 在区间 $[a,+\infty)$ 上是增函数
$\text{B.}$ 存在 $a \in R$ ,使得 $f(x)$ 为偶函数
$\text{C.}$ 若 $f(0)=f(2)$ ,则 $f(x)$ 的图象关于 $x=1$ 对称
$\text{D.}$ 若 $a^2-b-2>0$ ,则函数 $h(x)=f(x)-2$ 有 2 个零点
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知 $\alpha \in\left\{-2,-1,-\frac{1}{2}, \frac{1}{2}, 1,2,3\right\}$ ,若幂函数 $f(x)=x^\alpha$ 为奇函数,且在 $(0,+\infty)$ 上递减,则 $\alpha=$
已知二次函数 $f(x)$ 满足 $f(2)=-1, f(-1)=-1$ ,且 $f(x)$ 的最大值是 8 ,则 $f(x)=$
已知二次函数 $f(x)$ 的图象经过点 $(4,3)$ ,它在 $x$ 轴上截得的线段长为 2 ,并且对任意 $x \in R$ ,都有 $f(2-x)=f(2+x)$ ,则 $f(x)=$
已知 $y=f(x)$ 是奇函数,当 $x \geq 0$ 时,$f(x)=x^{\frac{2}{3}}$ ,则 $f(-8)$ 的值是
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知幂函数 $f(x)=x^{\frac{1}{2}}$ ,若 $f(a+1) < f(10-2 a)$ ,求实数 $a$ 的取值范围.
已知幂函数 $f(x)=x^{-1}$ ,若 $f(a+1) < f(10-2 a)$ ,求实数 $a$ 的取值范围.
若函数 $y=x^2-2 x+3$ 在区间 $[0, m]$ 上有最大值 3 ,最小值 2 ,求实数 $m$ 的取值范围.
求函数 $f(x)=x^2-2 a x$ 在区间 $[0,1]$ 上的最小值.
求函数 $y=a x^2-2 x+3(a \in R )$ 在区间 $[0,1]$ 上的最大值.
若函数 $y=x^2-2 x+3$ 在区间 $[0, m]$ 上有最大值 3 ,最小值 2 ,求实数 $m$ 的取值范围.
已知二次函数 $f(x)=a x^2+b x+c$ ,且满足 $f(0)=2, f(x+1)-f(x)=2 x+1$ .
(1)求函数 $f(x)$ 的解析式;
(2)当 $x \in[t, t+2](t \in R )$ 时,求函数 $f(x)$ 的最小值 $g(t)$(用 $t$ 表示).