单选题 (共 11 题 ),每题只有一个选项正确
下列各数中,绝对值最小的是
$\text{A.}$ -3
$\text{B.}$ -1
$\text{C.}$ 0
$\text{D.}$ 2
如图,若线段 $A B$ 与线段 $C D$ 有交点,则点 $D$ 应与下列哪个点重合
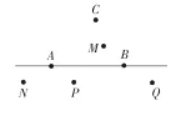
$\text{A.}$ 点 $P$
$\text{B.}$ 点 $N$
$\text{C.}$ 点 $M$
$\text{D.}$ 点 $Q$
下列运算结果与 $2^{-1}$ 相等的是
$\text{A.}$ $1-\frac{1}{2}$
$\text{B.}$ $-1-\frac{1}{2}$
$\text{C.}$ $-1 \times \frac{1}{2}$
$\text{D.}$ $-1 \times 2$
若 $m>n$ ,则 $2 m \square 2 n$ , $\square$ 中应填
$\text{A.}$ $ < $
$\text{B.}$ $=$
$\text{C.}$ $>$
$\text{D.}$ 无法确定
若 $a=\sqrt{2}+1, b=\sqrt{2}-1$ ,则 $\sqrt{a^2+3 a b+b^2}=$
$\text{A.}$ 2
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $\sqrt{7}$
$\text{D.}$ 3
某健康成年人心脏每分钟约跳 70 次,每分钟流过的血液量约为 $5 \times 10^3 ml$ ,则 5 分钟该成年人心脏流过的血液量用科学记数法表示约为
$\text{A.}$ $25 \times 10^3 ml$
$\text{B.}$ $2.5 \times 10^3 ml$
$\text{C.}$ $2.5 \times 10^6 ml$
$\text{D.}$ $0.25 \times 10^5 ml$
化简$$
\dfrac{\overbrace{4 \times 4 \times \cdots \times 4 \times 4}^{m}}{
\underbrace{2 \times 2 \times \cdots \times 2 \times 2}_m}
$$
的结果为
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ $4^{ m }$
$\text{D.}$ $2^m$
如图,这是由 4 个完全相同的小正方体组合而成的几何体,则该几何体的三视图中,完全相同的是
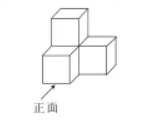
$\text{A.}$ 主视图和左视图
$\text{B.}$ 主视图和俯视图
$\text{C.}$ 左视图和俯视图
$\text{D.}$ 三种视图都相同
若 $1 < x < y$ ,则 $\frac{x}{y}-\frac{x-1}{y-1}$ 的值为
$\text{A.}$ 负数
$\text{B.}$ 非负数
$\text{C.}$ 0
$\text{D.}$ 正数
某校射击比赛所用的靶子有 8 环, 9 环, 10 环三个环次,每一环又有 10 个小环,小新,小华,小宇三人每人射击三次,成绩如图所示,则射击成绩的平均数约为 9.0 环的是
$\text{A.}$ 小新
$\text{B.}$ 小宇
$\text{C.}$ 小华
$\text{D.}$ 三人都有可能
如图,$M, N$ 为数轴上的两点,$P$ 为 $M N$ 的中点,点 $M, N$ 对应的数分别为 $m, n$ ,且 $m n>0$ .若将点 $N$ 沿原点翻折得到点 $N^{\prime}$ ,翻折后 $M N^{\prime}$ 的长度为 10 ,则点 $P$ 所对应的数为
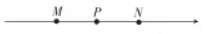
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ $\pm 4$
$\text{D.}$ $\pm 5$
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
课外兴趣小组进行一个混合运算题目的游戏,给出一个数,按照四位同学提供的运算方式及先后顺序运算,可得运算结果。
小齐:乘以 -4 。
小家:除以 2 。
小治:加上1.
小国:减去 $\Delta$ 。
(1)若给出的数字为 $-1, \Delta$ 为 -2 ,求运算结果.
(2)若给出的数为 3 ,运算结果为最大的负整数,求 $\Delta$ 表示的数.
当直角三角形的三边长都是正整数时,我们称这三个正整数为勾股数.
(1)若 $a, b$ 为一个直角三角形的两条直角边长,$c$ 为斜边长,$a, b, c$ 为勾股数,且 $a=n+7$ , $c=n+8, n$ 为正整数,求 $b$ 的值(用含 $n$ 的式子表示),并直接写出符合题意的最小的 $b$值.
(2)当 $n$ 是大于 1 的整数时,判断 $2 n, n^2-1, n^2+1$ 是否是勾股数,并说明理由.
嘉嘉在玩弹力球,琪琪据此出了一道数学题,请根据信息解答此题.如图,在平面直角坐标系中,嘉嘉在某处将球掷出后第一次落地点在原点 $O$ 处,第一次反弹后,弹力球的运动路径符合函数 $y=a x^2+b x$ 的图象的一部分.小球在距第一次落地点 $O$ 水平距离为 1 m 处时,高度为 3 m 。第二次落地点 $C$ 与第一次落地点 $O$ 的距离为 4 m ,弹力球第二次反弹后,运动路径也是拋物线,且飞行的最大高度和水平距离都为第一次的一半。
(1)求第一次反弹后,弹力球运动路径的函数解析式,并直接写出路径顶点 $A$ 的坐标.
(2)若在距离原点 5.5 m 处放置一块高度为 1.6 m 的挡板,请通过计算判断弹力球是否会碰到挡板.
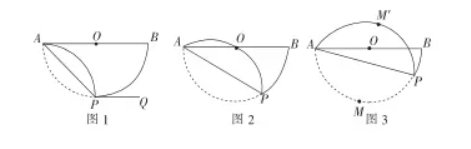
如图,珍珍利用一张直径 $A B$ 为 8 cm 的半圆形纸片探究圆的知识。将半圆形纸片沿弦 $A P$ 折叠。
(1)如图 1,$P Q$ 为 $\odot O$ 的切线,当 $\angle P A B=45^{\circ}$ 时,求证:$P Q / / A B$ .
(2)如图 2,当 $\angle P A B=30^{\circ}$ 时,通过计算比较 $A P$ 与 $\overparen{B P}$ 哪个长度更长.( $\pi$ 取 $3.14, \sqrt{3} \approx 1.73$ )
(3)如图 3.$M$ 为 $\widehat{A P}$ 的中点,$M$ 为点 $M$ 关于弦 $A P$ 的对称点,当 $\angle P A B=15^{\circ}$ 时,直接写出点 $M$ 与点 $M'$之间的距离约为 $\qquad$ cm .(结果保留两位小数,参考数据: $\sin 15^{\circ} \approx 0.26, \tan 15^{\circ} \approx 0.27$)