单选题 (共 5 题 ),每题只有一个选项正确
设 $P(A)>0, P(B)>0$ 则下列叙述正确的选项是
$\text{A.}$ 若 $A$ 与 $B$ 互不相容, 则它们相互独立
$\text{B.}$ 若 $A$ 与 $B$ 相互独立, 则它们互不相容
$\text{C.}$ $A 、 B$ 互不相容与相互独立不可能同时成立
$\text{D.}$ $P(A)=P(B)=0.7$ 且 $A$ 与 $B$ 互不相容
设离散型随机变量 $X$ 的分布函数 $F(x)=\left\{\begin{array}{cc}0 & x < 0 \\ a & 0 \leq x < 2 \\ \frac{3}{4}-a & 2 \leq x < 3 \\ a+b & x \geq 3\end{array}\right.$, 且 $P(X=3)=\frac{1}{2}$ 则 $a, b$ 的值分别为
$\text{A.}$ $\frac{1}{3}, \frac{1}{6}$
$\text{B.}$ $\frac{1}{6}, \frac{1}{3}$
$\text{C.}$ $\frac{1}{3}, \frac{2}{3}$
$\text{D.}$ $\frac{1}{4}, \frac{3}{4}$
设随机变量 $X \sim U[-1,1]$, 数学期望 $E ( Y )=\frac{1}{2}$, 且 $X, Y$ 相互独立, 则 $E(X Y+2 Y)=$
$\text{A.}$ 1
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 0
$\text{D.}$ $-\frac{1}{2}$
设 $(X, Y)$ 服从区域 $D$ 上的均匀分布, 其中 $D=\{(x, y) \mid x \geq 0,0 \leq y \leq-x+1\}$,则 $P\left(X < \frac{1}{2}, Y < \frac{1}{2}\right)=$
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ 以上选项都不对
设 $X$ 是随机变量, $x_0$ 为任意实数, $E(X)$ 是 $X$ 的数学期望, 则正确的选项是
$\text{A.}$ $E\left(X-x_0\right)^2=E[X-E(X)]^2$
$\text{B.}$ $E\left(X-x_0\right)^2 \geq E[X-E(X)]^2$
$\text{C.}$ $E\left(X-x_0\right)^2 < E[X-E(X)]^2$
$\text{D.}$ $E\left(X-x_0\right)^2=0$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
已知 $P(A)=P(B)=0.4, P(A \bar{B})=0.3$, 则 $P(A B)= , P(A \cup B)= $.
设 $X \sim$ 泊松分布 $P(\lambda), E(X-2)=0$, 则 $D(4 X-1)=, P(X \geq 2)=$.
设随机变量 $X \sim N\left(5,3^2\right)$, 则 $Y=\underline{\frac{X-5}{3}} \sim N(0,1), P\{4 < X < 6\}=$ (已知 $\Phi(0.11)=0.5438, \Phi(0.33)=0.6293$ )。
已知随机变量 $X$ 的分布函数 $F(x)=A+B \arctan x,(-\infty < x < +\infty)$, 则系数 $A=, B=$.
将三个不同的球随机放入 4 个杯子中, 则杯中球的最大个数为 2 的概率为 .
设 $X \sim N\left(-1,4^2\right), \quad Y \sim N\left(-1,3^2\right)$ 且 $X$ 和 $Y$ 相互独立, 则由切比雪夫不等式估计概率 $p=P(|X-Y| < 10)$可得 $p \geq$ $\qquad$ .
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
将两信息分别编码 $M$ 和 $N$ 传送出去, 接收站收到时, $M$ 被误收作 $N$ 的概率为 0.02 , 而 $N$ 被误收为 $M$的概率为 0.01 . 信息 $M$ 与信息 $N$ 传送的频繁程度为 $2: 1$. 若接收站收到的信息是 $M$, 问原发信息是 $M$ 的概率是多少? (必须写出题设、已知的概率和所用的概率公式, 并计算结果 (用分数表示))
一袋子里有 5 只球, 编号为 $1,2,3,4,5$, 从中一次性地任取三只, 记 $X$ 是所取三只球的最大号码,
求:(1) $X$ 的分布律和分布函数 $F(x)$ ;(2) $P\{X=4 \mid X>3.1\}$ ;(3) $D(X)$.
已知连续型随机变量 $X$ 的概率密度 $f(x)=\left\{\begin{array}{cc}k x, & 0 < x < 2 \\ 0 & \text { 其他 }\end{array}\right.$, 用 $Y$ 表示对 $X$ 的 3 次独立重复观察中 $\{X \leq 1\}$ 事件出现的次数, 求: (1) 系数 $k$; (2) $E\left(\frac{1}{X}+4\right)$; (3) $P(Y>1)$.
设随机变量 $X \sim U[1,3]$, 求 $Y=X^3$ 的分布函数 $F_Y(y)$ 与概率密度函数 $f_Y(y)$.
已知随机变量X与Y的概率分布为
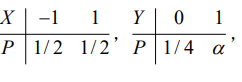
且 $P\{X=Y\}=\frac{1}{2}$, 试求: (1) $\alpha$ 的值及 $(X, Y)$ 的分布律; (2) 判断 $X$ 和 $Y$ 是否相互独立; (3) 其分布函数在点 $(1,0)$ 的值 $F(1,0)$; (4) $Z=X Y$的分布律.
设 $X$ 与 $Y$ 相互独立, 概率密度分别为 $f_1(x)=\left\{\begin{array}{l}e^{-x}, x>0 \\ 0, \\ x \leq 0\end{array}, \quad f_2(y)=\left\{\begin{array}{ll}e^{-y}, & y>0 \\ 0, & y \leq 0\end{array}\right.\right.$,
求: (1) $(X, Y)$ 的联合概率密度; (2) $P\{Y+X \leq 1\}$; (3) $Z=X+Y$ 的概率密度.
设连续型随机变量 $X$ 的数学期望 $E(X)$ 存在, 若对常数 $c$ 恒有 $P(X \geq c)=1$, 证明: $E(X) \geq c$.