单选题 （共 10 题 ），每题只有一个选项正确
设 $A$ 为 $m \times n$ 矩阵, 则齐次线性方程组 $A x = 0$ 仅有零解的充分条件是
$\text{A.}$ $A$ 的列向量线性无关.
$\text{B.}$ $A$ 的列向量线性相关.
$\text{C.}$ $A$ 的行向量线性无关.
$\text{D.}$ $A$ 的行向量线性相关.
设 $A$ 是四阶矩阵, $A$ * 是 $A$ 的伴随矩阵, 若线性方程组 $A x = 0$ 的基础解系中只有 2个向量, 则 $A ^*$ 的秩是
$\text{A.}$ 0 .
$\text{B.}$ 1 .
$\text{C.}$ 2 .
$\text{D.}$ 3 .
非齐次线性方程组 $A x = b$ 中未知量个数为 $n$, 方程个数为 $m$, 系数矩阵 $A$ 的秩为 $r$, 则
$\text{A.}$ $r=m$ 时, 方程组 $A x = b$ 有解.
$\text{B.}$ $r=n$ 时,方程组 $A x = b$ 有唯一解.
$\text{C.}$ $m=n$ 时,方程组 $A x = b$ 有惟一解.
$\text{D.}$ $r < n$ 时, 方程组 $A x = b$ 有无穷多解.
设矩阵 $A =\left(\begin{array}{ccc}1 & 1 & 1 \\ 1 & 2 & a \\ 1 & 4 & a^2\end{array}\right), b =\left(\begin{array}{c}1 \\ d \\ d^2\end{array}\right)$, 若集合 $\Omega=\{1,2\}$, 则线性方程组 $A x = b$ 有无穷多解的充分必要条件为
$\text{A.}$ $a \notin \Omega, d \notin \Omega$.
$\text{B.}$ $a \notin \Omega, d \in \Omega$.
$\text{C.}$ $a \in \Omega, d \notin \Omega$.
$\text{D.}$ $a \in \Omega, d \in \Omega$.
设 $A$ 是 $m \times n$ 矩阵, $A x = x$ 是非齐次线性方程组 $A x = b$ 所对应的齐次线性方程组, 则下列结论正确的是
$\text{A.}$ 若 $A x = 0$ 仅有零解, 则 $A x = b$ 有唯一解.
$\text{B.}$ 若 $A x = 0$ 有非零解, 则 $A x = b$ 有无穷多个解.
$\text{C.}$ 若 $A x = b$ 有无穷多个解, 则 $A x = 0$ 仅有零解.
$\text{D.}$ 若 $A x = b$ 有无穷多个解, 则 $A x = 0$ 有非零解.
设有齐次线性方程组 $A x = 0$ 和 $B x = 0$, 其中 $A , B$ 均为 $m \times n$ 矩阵, 现有 4 个命题：
(1) 若 $A x = 0$ 的解均是 $B x = 0$ 的解, 则 $r ( A ) \geqslant r ( B )$;
(2) 若 $r ( A ) \geqslant r ( B )$, 则 $A x = 0$ 的解均是 $B x = 0$ 的解;
(3) 若 $A x = 0$ 与 $B x = 0$ 同解, 则 $r ( A )= r ( B )$;
(4) 若秩 $r ( A )= r ( B )$, 则 $A x = 0$ 与 $B x = 0$ 同解。
以上命题中正确的是
$\text{A.}$ (1)(2).
$\text{B.}$ (1) (3).
$\text{C.}$ (2)(4).
$\text{D.}$ (3) (4).
已知 $\beta _1, \beta _2$ 是非齐次线性方程组 $A x = b$ 的两个不同的解, $\alpha _1, \alpha _2$ 是对应齐次线性方程组 $A x = 0$ 的基础解系， $k_1, k_2$ 为任意常数，则方程组 $A x = b$ 的通解（一般解）是
$\text{A.}$ $k_1 \alpha _1+k_2\left( \alpha _1+ \alpha _2\right)+\frac{ \beta _1- \beta _2}{2}$.
$\text{B.}$ $k_1 \alpha _1+k_2\left( \alpha _1- \alpha _2\right)+\frac{ \beta _1+ \beta _2}{2}$.
$\text{C.}$ $k_1 \alpha _1+k_2\left( \beta _1+ \beta _2\right)+\frac{ \beta _1- \beta _2}{2}$.
$\text{D.}$ $k_1 \alpha _1+k_2\left( \beta _1- \beta _2\right)+\frac{ \beta _1+ \beta _2}{2}$.
设 $\alpha _1, \alpha _2, \alpha _3$ 是四元非齐次线性方程组 $A X = b$ 的三个解向量, 且 $r ( A )=3, \alpha _1=$ $(1,2,3,4)^{ T }, \alpha _2+ \alpha _3=(0,1,2,3)^{ T }, c$ 表任意常数, 则线性方程组 $A X = b$ 的通解 $X =$
$\text{A.}$ $\left(\begin{array}{l}1 \\ 2 \\ 3 \\ 4\end{array}\right)+c\left(\begin{array}{l}1 \\ 1 \\ 1 \\ 1\end{array}\right)$.
$\text{B.}$ $\left(\begin{array}{l}1 \\ 2 \\ 3 \\ 4\end{array}\right)+c\left(\begin{array}{l}0 \\ 1 \\ 2 \\ 3\end{array}\right)$.
$\text{C.}$ $\left(\begin{array}{l}1 \\ 2 \\ 3 \\ 4\end{array}\right)+c\left(\begin{array}{l}2 \\ 3 \\ 4 \\ 5\end{array}\right)$.
$\text{D.}$ $\left(\begin{array}{l}1 \\ 2 \\ 3 \\ 4\end{array}\right)+c\left(\begin{array}{l}3 \\ 4 \\ 5 \\ 6\end{array}\right)$.
设有三张不同平面的方程 $a_{i 1} x+a_{i 2} y+a_{i 3} z=b_i, i=1,2,3$, 它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为 2 , 则这三张平面可能的位置关系为
$\text{A.}$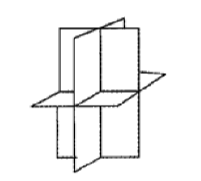 
$\text{B.}$ 
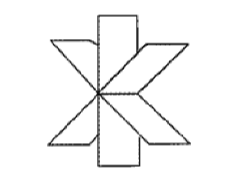$\text{C.}$ 
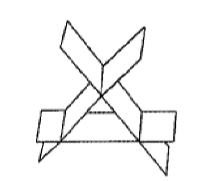$\text{D.}$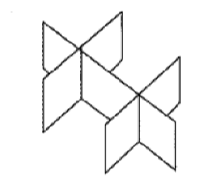 
如图所示, 有 3 张平面两两相交, 交线相互平行, 它们的方程
$$
a_{i 1} x+a_{i 2} y+a_{i 3} z=d_i(i=1,2,3)
$$
组成的线性方程组的系数矩阵和增广矩阵分别记为 $A , \overline{ A }$, 则
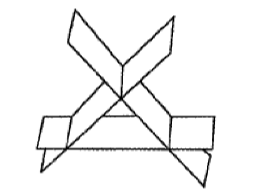
$\text{A.}$ $r ( A )=2, r (\overline{ A })=3$.
$\text{B.}$ $r ( A )=2, r ( A )=2$.
$\text{C.}$ $r ( A )=1, r (\overline{ A })=2$.
$\text{D.}$ $r ( A )=1, r (\overline{ A })=1$.